BU KONUDA ÖĞRENECEKLERİMİZ:
✓ Dikdörtgenler prizmasının yüzey alanı
✓ Kare prizmanın yüzey alanı
✓ Küpün yüzey alanı
Bir kutuyu renkli kağıtla kaplayıp hediye paketi yaparken kutunun tüm yüzlerini kaplarız ve kaplanan alan bu kutunun yüzey alanıdır. Önceki konularda dikdörtgenler prizmasının temel elemanları ve dikdörtgenler prizmasının açınımını öğrenmiştik. Bu konuda ise dikdörtgenler prizmasının alanını, kare prizmanın alanını ve küpün alanını öğreneceğiz.
DİKDÖRTGENLER PRİZMASININ ALANI
Dikdörtgenler prizmasının yüzey alanı bulunurken tüm yüzlerin alanları bulunur ve toplanır. Dikdörtgenler prizmasında karşılıklı yüzeylerin alanları birbirine eşittir.
ÖRNEK: Aşağıdaki dikdörtgenler prizmasının yüzey alanını bulalım.
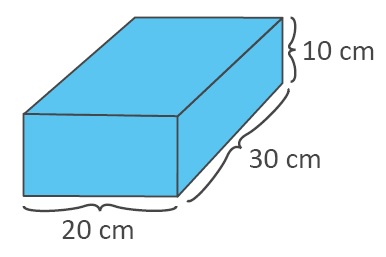
1. YOL: Dikdörtgenler prizmasının alanını bulurken tüm yüzlerdeki dikdörtgenlerin alanlarını bulup toplayacağız. Bunu yaparken ön yüz ile arka yüz, sağ yüz ile sol yüz, üst yüz ile alt yüzün alanlarının eşit olduğundan da faydalanacağız.
Ön yüzün alanı = 20 x 10 = 200 cm2
Sağ yüzün alanı = 30 x 10 = 300 cm2
Üst yüzün alanı = 30 x 20 = 600 cm2
Dikdörtgenler Prizmasının Alanı = Ön + Arka + Sağ + Sol + Üst + Alt
Dikdörtgenler Prizmasının Alanı = 200 + 200 + 300 + 300 + 600 + 600
Dikdörtgenler Prizmasının Alanı = 2200 cm2
2. YOL: Dikdörtgenler prizmasının alanını, açınımındaki dikdörtgenlerin alanlarını hesaplayıp toplayarak da bulabiliriz.

KARE PRİZMANIN ALANI
Kare prizmanın yüzey alanı bulunurken tüm yüzlerin alanları bulunur ve toplanır. Kare prizmada taban alanları birbirine eşittir ve tüm yanal yüzlerin alanları birbirine eşittir.
ÖRNEK: Aşağıdaki kare prizmanın yüzey alanını bulalım.

1. YOL: Kare prizmanın alanını bulurken tüm yüzlerin alanlarını bulup toplayacağız. Bunu yaparken taban alanlarının birbirine eşit ve tüm yanal yüzlerin alanlarının birbirine eşit olduğundan da faydalanacağız.
Bir tabanın alanı = 12 x 12 = 144 cm2
Bir yanal yüzün alanı = 12 x 15 = 180 cm2
2 tabanın toplam alanı = 144 x 2 = 288 cm2
4 yanal yüzün toplam alanı = 180 x 4 = 720 cm2
Kare Prizmanın Alanı = Taban Alanları + Yanal Yüz Alanları
Kare Prizmanın Alanı = 288 + 720 = 1008 cm2
2. YOL: Kare prizmanın alanını, açınımındaki kare ve dikdörtgenlerin alanlarını hesaplayıp toplayarak da bulabiliriz.

KÜPÜN ALANI
Küpün yüzey alanı bulunurken tüm yüzlerin alanları bulunur ve toplanır. Küpte tüm yüzlerin alanları birbirine eşittir.
ÖRNEK: Aşağıdaki küpün yüzey alanını bulalım.

1. YOL: Küpün tüm yüzlerinin alanları birbirine eşit olduğu için bir yüzünün alanını buluruz ve 6 ile çarparız.
Bir yüzünün alanı = 10 x 10 = 100 cm2
Küpün Alanı = 100 x 6 = 600 cm2
2. YOL: Küpün alanını, açınımındaki karelerin alanlarını hesaplayıp toplayarak da bulabiliriz.

KONUYU PEKİŞTİRMEK İÇİN:
İLGİLİ KAZANIM TESTİ BAĞLANTISI
KONU KAZANIMLARI
BU KONUYLA İLGİLİ KAZANIMLAR:
✓ Dikdörtgenler prizmasının yüzey alanını hesaplamayı gerektiren problemleri çözer.
| ÖNCEKİ KONU | SONRAKİ KONU |
| Dikdörtgenler Prizmasının Açınımı | 5. Sınıf Matematik Testleri |
