BU KONUDA ÖĞRENECEKLERİMİZ:
✓ Çarpanlara Ayırma
✓ Ortak Çarpan Parantezine Alma
✓ Gruplandırarak Çarpanlara Ayırma
✓ Özdeşliklerden Faydalanarak Çarpanlara Ayırma
✓ ax2 + bx + c Şeklindeki İfadeleri Çarpanlara Ayırma
CEBİRSEL İFADELERİ ÇARPANLARA AYIRMA
Bir cebirsel ifadeyi çarpanlarının çarpımı şeklinde yazmaya, o cebirsel ifadeyi çarpanlara ayırma denir.
Cebirsel ifadeler çarpanlara ayrılırken farklı yöntemlerden faydalanılır.
1) Ortak Çarpan Parantezine Alma
Bir cebirsel ifadeyi ortak çarpan parantezine alarak çarpanlara ayırmak istiyorsak cebirsel ifadedeki her terimde ortak olarak bulunan bir çarpan bulmalıyız. Bu ortak çarpan parantezin dışına yazılır ve parantezin içine de verilen ifadedeki terimlerin ortak çarpana bölümleri yazılır.
ÖRNEK: 3x + 6 ifadesini çarpanlarına ayıralım.
Bu ifade iki terimli bir ifadedir ve bu iki terimde de 3 çarpanı vardır. Ortak çarpan parantezine şu şekilde alırız:
3x + 6 = 3.x + 3.2 = 3.(x + 2)
ÖRNEK: 6x2 + 4x ifadesini çarpanlarına ayıralım.
İki terimde de 2x çarpan olarak vardır. Bu yüzden ortak çarpan parantezine şu şekilde alınır:
6x2 + 4x = 2x.3x + 2x.2 = 2x.(3x + 2)
ÖRNEK: 4x3 + 12x2 − 8x ifadesini çarpanlarına ayıralım.
Bu üç terimli ifadede her ifadede ortak olan çarpan 4x’tir.
4x3 + 12x2 − 8x = 4x.x2 + 4x.3x − 4x.2 = 4x.(x2 + 3x − 2)
2) Gruplandırarak Çarpanlara Ayırma
Ortak çarpan parantezine alınarak çarpanlara ayırma işlemi yapılamayan durumlarda gruplandırarak çarpanlara ayırma yöntemi kullanılabilir. Bu yöntemde terimler kendi aralarında ortak çarpan bulunacak şekilde iki veya daha fazla terimden oluşan gruplara ayrılır. Daha sonra ortak çarpan parantezine alınır. Gruplandırarak çarpanlara ayırma üçten fazla terimi olan cebirsel ifadelerde kullanılır.
ÖRNEK: ab + bc + ac + c2 ifadesini çarpanlarına ayıralım.
Cebirsel ifadeye baktığımızda 4 terimin hepsinin ortak bir çarpanı bulunmamaktadır. Bu ifadeyi gruplandırarak çarpanlara ayrılır. İlk iki terim b parantezine son iki terim c parantezine alınır. Sonra ortak çarpan parantezine alırız.
ab + bc + ac + c2
= b.a + b.c + c.a + c.c
= b.(a + c) + c.(a + c)
= (a + c).(b + c)
ÖRNEK: 4ay − 3by + 8ac − 6bc ifadesini çarpanlara ayıralım.
Cebirsel ifadeye baktığımızda 4 terimin hepsinin ortak bir çarpanı bulunmamaktadır. Bu ifadeyi gruplandırarak çarpanlara ayrılır. İlk iki terim y parantezine son iki terim 2c parantezine alınır. Sonra ortak çarpan parantezine alırız.
4ay − 3by + 8ac − 6bc
= y.4a − y.3b + 2c.4a − 2c.3b
= y.(4a − 3b) + 2c.(4a − 3b)
=(y + 2c).(4a − 3b)
3) İki Kare Farkı Özdeşliğinden Faydalanarak Çarpanlara Ayırma
Bazı ifadeler Özdeşlik konusunda öğrendiğimiz iki kare farkı özdeşliği kullanarak çarpanlara ayrılabilir. Cebirsel ifadedeki iki terim de eğer tam kare ise bu iki terimin kareköklerinin toplamı ile farkı çarpılır.
► x2 − y2 = (x − y).(x + y)
ÖRNEK: x2 − 25 ifadesini çarpanlarına ayıralım.
x2 − 25 = (x − 5).(x + 5)
ÖRNEK: 4y2 − 36 ifadesini çarpanlarına ayıralım.
4y2 − 36 = (2y − 6).(2y + 6)
4) Tam Kare Özdeşliklerinden Faydalanarak Çarpanlara Ayırma
Bazı ifadeler Özdeşlik konusunda öğrendiğimiz tam kare özdeşlikleri kullanarak çarpanlara ayrılabilir. Cebirsel ifadedeki birinci terimin karekökü ile üçüncü terimin karekökünün çarpımının iki katı ortanca terimi veriyorsa bu cebirsel ifade bir tam karedir. Çarpanları ise birinci terimin karekökü ile ikinci terimin karekökünün toplamının karesidir (veya farkının karesidir).
► x2 + 2xy + y2 = (x + y).(x + y)
► x2 − 2xy + y2 = (x − y).(x − y)
ÖRNEK: x2 + 6x + 9 ifadesini çarpanlarına ayıralım.
İfadesinin ilk terimi x2 ve üçüncü terimi 9’dur.
Bu terimlerin karekökleri x ve 3’tür.
Ortadaki terim ise bu kareköklerin çarpımının iki katıdır.
Bu sebeple bu ifade bir tam karedir ve çarpanlara şu şekilde ayrılır:
x2 + 6x + 9 = (x + 3)2 = (x + 3).(x + 3)
ÖRNEK: 25x2 − 20xy + 4y2 ifadesini çarpanlarına ayıralım.
İfadesinin ilk terimi 25x2 ve üçüncü terimi 4y2‘dir.
Bu terimlerin karekökleri 5x ve 2y’dir.
Ortadaki terim ise bu kareköklerin çarpımının iki katıdır.
Bu sebeple bu ifade bir tam karedir ve çarpanlara şu şekilde ayrılır:
25x2 − 20xy + 4y2 = (5x + 2y)2 = (5x + 2y).(5x + 2y)
5) ax2 + bx + c Formundaki İfadeleri Çarpanlara Ayırma
ax2 + bx + c şeklindeki ifadeleri çarpanlara ayırma 8. sınıf müfredatında yer almamaktadır.
Bu şekildeki ifadelerin çarpanlara nasıl ayrıldığını merak ediyorsanız aşağıdaki bölümden öğrenebilirsiniz.
ax2 + bx + c üç terimli cebirsel ifade çarpanlara ayrılırken ax2 ve c’nin çarpanları, çapraz çarpımlarının toplamı bx’i verecek şekilde altlarına yazılır. Yazılan çarpanların karşılıklı toplamları verilen ifadenin çarpanlarını oluşturur.
ÖRNEK: x2 + 5x + 6 ifadesini çarpanlarına ayıralım.
Bu ifadedeki x2 ve 6 ‘yı çarpanlarına ayıralım. Burada ayırırken çarpaz çarpıp toplandığında ortadaki ifadeyi vermesi gerektiğini unutmamalıyız ve ona göre çarpan seçmeliyiz.
x2 = x . x ve +6 = 3 . 2 olsun. Burada 6 = (−3).(−2) şeklinde de yazabilirdik ancak ortadaki ifadeye göre seçmek durumundayız.
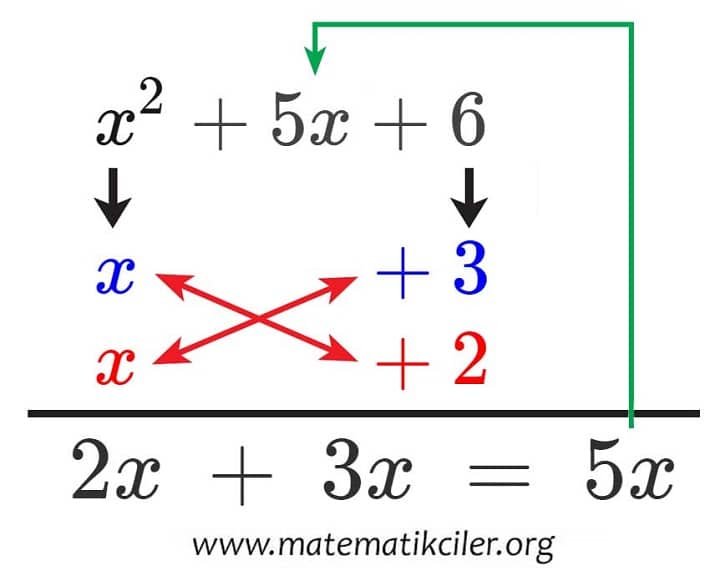
Her iki terimin çarpanlarını altlarına yazdık ve çapraz çarpıp topladığımızda ortadaki terimi vermesini sağladık. Son olarak bu üç terimli cebirsel ifadenin çarpanlara ayrılmış şeklini yazmalıyız. Çarpanlara ayrılmış şeklini yazarken yan yana bulunan ifadeleri toplayacağız ve bunları çarpacağız. Yani resimdeki mavi kısım ile kırmızı kısımı çarpacağız.
x2 + 5x + 6 = (x + 3).(x + 2)
ÖRNEK: 2x2 + 7x − 15 ifadesini çarpanlarına ayıralım.
Birinci ve üçüncü terimin altına çarpanlarını yazarken uygun çarpanlar seçmeli ve çarpaz çarpılıp toplanınca ortadaki terimi vermesi gerektiğini unutmamalıyız. Buna göre bu ifade şu şekilde çarpanlarına ayrılırdı.

Her iki terimin çarpanlarını altlarına yazdık ve çapraz çarpıp topladığımızda ortadaki terimi vermesini sağladık. Son olarak bu üç terimli cebirsel ifadenin çarpanlara ayrılmış şeklini yazmalıyız. Çarpanlara ayrılmış şeklini yazarken yan yana bulunan ifadeleri toplayacağız ve bunları çarpacağız. Yani resimdeki mavi kısım ile kırmızı kısımı çarpacağız.
2x2 + 7x − 15 = (2x −3).(x + 5)
KONUYU PEKİŞTİRMEK İÇİN:
İLGİLİ ÇALIŞMA KAĞIDI BAĞLANTISI
İLGİLİ KAZANIM TESTİ BAĞLANTISI
TEST ÇÖZME BAĞLANTISI
KONU KAZANIMLARI
BU KONUYLA İLGİLİ KAZANIMLAR:
✓ Cebirsel ifadeleri çarpanlarına ayırır.
| ÖNCEKİ KONU | SONRAKİ KONU |
| Özdeşlikler | Cebir Karoları ile Çarpanlara Ayırma |
