Sayı Örüntüleri (Aritmetik Dizi, Geometrik Dizi, Özel Sayı Örüntüleri)

Sayı örüntüleri konusuna daha önceki yıllardan aşinayız. Belirli bir kurala göre devam eden sayıların oluşturduğu örüntüye sayı örüntüleri diyorduk. Burada ise sayı dizinin ne olduğunu, aritmetik ve geometrik dizileri ve özel sayı örüntülerini öğreneceğiz.

SAYI DİZİSİ NEDİR?

# Sayıların virgülle ayrılarak birbiri ardına dizilmesine sayı dizisi denir. Dizideki her bir sayıya dizinin terimi denir.

ÖRNEK-1: 1, 3, 5, 7, 9, 11, 13, … dizisi tek sayılardan oluşan ve 1’den başlayarak ikişer ikişer artan bir sayı dizisidir.

ÖRNEK-2: 1, 3, 9, 27, 81, 243, … dizisi 1’den başlayıp üçer üçer katlanarak devam eden bir sayı dizisidir.

ARİTMETİK SAYI DİZİSİ NEDİR?

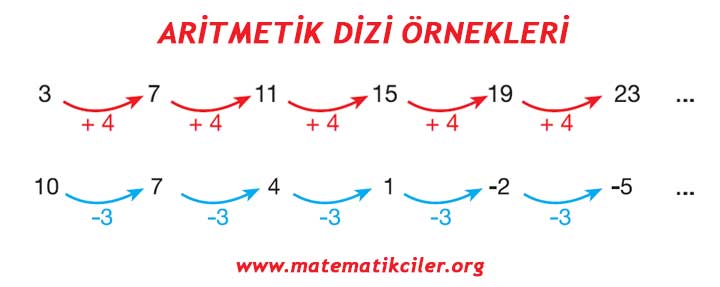
# Bir sayı dizisindeki ardışık iki terim arasındaki fark sabit bir sayı ise bu diziye aritmetik dizi denir. Örneğin yukarıda verdiğimiz Örnek-1’deki tek sayılar dizisi aritmetik bir dizidir çünkü ardışık terimler arasındaki fark sabittir.

# Aritmetik dizide ardışık iki terim arasındaki farka dizinin ortak farkı denir. Tek sayılar dizisinde dizinin ortak farkı 2’dir. Dizinin ortak farkı bulunurken herhangi bir terimden bir önceki terim çıkartılır.

ARİTMETİK DİZİNİN GENEL TERİMİ NASIL BULUNUR?

Aritmetik dizinin genel terimi şu mantıkla bulunabilir. Örneğin 1’den başlayan ve ortak farkı 4 olan (yani dörder dörder artan) bir dizi oluşturalım. Bu dizinin terimleri şu şekilde olur:

1. terim:   1

2. terim:   5 = 1 + 4

3. terim:   9 = 1 + 4 + 4

4. terim: 13 = 1 + 4 + 4 + 4

görüldüğü gibi her bir terimi oluştururken aslında ilk terimden yola çıkıyoruz ve dizinin ortak farkını ekleyerek devam ediyoruz. Dizinin ortak farkını terim sayısının bir eksiği kadar ekliyoruz. Bu mantıkla mesela 10. terimi bulalım.

10. terim: 1 + 9 tane 4 = 1 + 9 . 4  = 1 + 36 = 37

ARİTMETİK DİZİ GENEL TERİM FORMÜLÜ:

İlk terimi a₁ olan ve ortak farkı r olan bir aritmetik dizinin genel terimi:

a_n = a₁ + (n-1) . r

GEOMETRİK SAYI DİZİSİ NEDİR?

# Bir sayı dizisindeki ardışık iki terim arasındaki oran sabit bir sayı ise bu diziye geometrik dizi denir. Örneğin yukarıda verdiğimiz Örnek-2’deki dizi geometrik bir dizidir çünkü ardışık terimler arasındaki oran sabittir.

# Geometrik dizide ardışık iki terim arasındaki orana dizinin ortak çarpanı denir. Örnek-2’deki dizinin ortak çarpanı 3’tür. Ortak çarpan bulunurken herhangi bir terim bir önceki terime bölünür.

GEOMETRİK DİZİNİN GENEL TERİMİ NASIL BULUNUR?

Geometrik dizinin genel terimi şu mantıkla bulunabilir. Örneğin 1’den başlayan ve ortak çarpanı 2 olan (yani ikiye katlanarak devam eden) bir dizi oluşturalım. Bu dizinin terimleri şu şekilde olur:

1. terim:   1

2. terim:   2 = 1 x 2

3. terim:   4 = 1 x 2 x 2

4. terim:   8 = 1 x 2 x 2 x 2

görüldüğü gibi her bir terimi oluştururken aslında ilk terimden yola çıkıyoruz ve dizinin ortak çarpanıyla çarparak devam ediyoruz. Dizinin ortak çarpanını terim sayısının bir eksiği kadar çarpıyoruz. Bu mantıkla mesela 10. terimi bulalım.

10. terim: 1 x 9 tane 2’nin çarpımı = 1 x 2⁹  = 1 x 512 = 512

GEOMETRİK DİZİ GENEL TERİM FORMÜLÜ:

İlk terimi a₁ olan ve ortak çarpanı r olan bir geometrik dizinin genel terimi:

a_n = a¹ . r^(n-1)

ÖZEL SAYI ÖRÜNTÜLERİ

ÜÇGENSEL SAYILAR

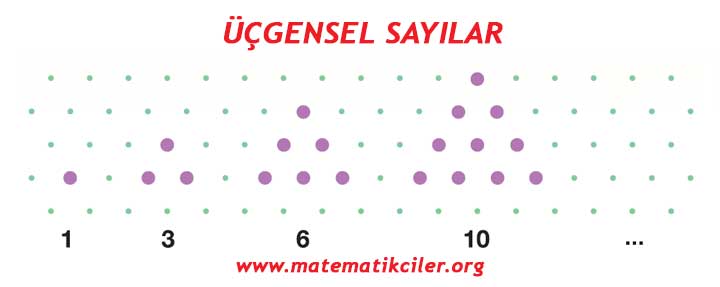
# 1’den n’ye kadar olan n doğal sayının toplamı şeklinde yazılabilen sayılara üçgensel sayılar denir. Bu sayılarla oluşturulmuş örüntüye ise üçgensel sayı dizisi denir.

Yukarıdaki tanımı örneklendirecek olursak:

1 üçgensel sayıdır.

3 üçgensel sayıdır çünkü 3 = 1+2

6 üçgensel sayıdır çünkü 6 = 1+2+3

bu listeyi bu şekilde uzatabiliriz.

# Üçgensel sayıları bir örüntü şeklinde yazacak olursak: 1, 3, 6, 10, 15, 21, 28, 36, …

KARESEL SAYILAR

#  Bir tam sayının karesi şeklinde yazılabilen sayılara tam kare sayılar veya karesel sayılar denir. Bu sayılarla oluşturulmuş örüntüye ise karesel sayı dizisi denir.

Yukarıdaki tanımı örneklendirecek olursak:

1 karesel sayıdır çünkü 1 = 1²

4 karesel sayıdır çünkü 4 = 2²

9 karesel sayıdır çünkü 9 = 3²

bu listeyi bu şekilde uzatabiliriz.

# Karesel sayıları bir örüntü şeklinde yazacak olursak: 1, 4, 9, 16, 25, 36, 49, 64, …

 FİBONACCİ SAYI DİZİSİ

Fibonacci sayıları İtalyan matematikçi Leonardo Fibonacci’nin ortaya koyduğu bir sayı dizisidir. Fibonacci sayı dizisi ilk iki terim hariç her terimin kendisinden önceki iki terimin toplanmasıyla oluşturulan bir dizidir.

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, … şeklinde devam eder.

Fibonacci bu sayı dizisini bir probleme çözüm ararken bulmuştur ve bu dizinin bir çok özelliği vardır. Daha fazla bilgi için sitemizde özel kategori açtığımız bölüme bakabilirsiniz:

FİBONACCİ SAYI DİZİSİ

PASCAL ÜÇGENİ

Fransız matematikçi Blaise PASCAL’ın sayı üçgeni üzerinde çok çalışması vardır. Bu sebeple sayıların toplanarak aşağıya doğru genişleşletilmesine dayanan piramit şeklindeki sayı üçgenine Paskal Üçgeni denilmektedir. Pascal üçgendeki sayılar arasındaki örüntüleri 1653 sayfalık bir çalışmada anlatmıştır. Farklı kaynaklarda bu sayı üçgenini Ömer HAYYAM’ın da incelediği belirtilmektedir. Bu sayı üçgenine Hayyam Üçgeni de denmektedir.

Pascal üçgeni binom açınımında, olasılıkta, kümelerde kullanılan bir sayı üçgenidir.

Yazar: www.matematikciler.com