Üçgen Çizimleri

BU KONUDA ÖĞRENECEKLERİMİZ:
✓ Kenar Uzunlukları Verilen Üçgeni Çizme
✓ Bir Kenar Uzunluğu ve İki Açının Ölçüsü Verilen Üçgeni Çizme
✓ Bir Açısının Ölçüsü ve İki Kenar Uzunlukları Verilen Üçgeni Çizme

ÜÇGEN ÇİZİMİ İÇİN GEREKLİ ŞARTLAR

Üçgenin temel elemanları, kenarları ve açılarıdır. Belirli bir üçgenin çizilebilmesi için bu temel elemanlardan en az üç tanesi bilinmeli ve bu bilgilerden en az biri kenar uzunluğu olmalıdır.

Üç kenar uzunluğu, iki kenar uzunluğu ile bu kenar arasındaki açının ölçüsü veya bir kenarının uzunluğu ile iki açısının ölçüsü verilen bir üçgen cetvel, açıölçer ve pergel kullanılarak çizilebilir.

Şimdi yeterli elemanı verilen üçgenler nasıl çizilir öğrenelim.

ÜÇGEN ÇİZİMLERİ

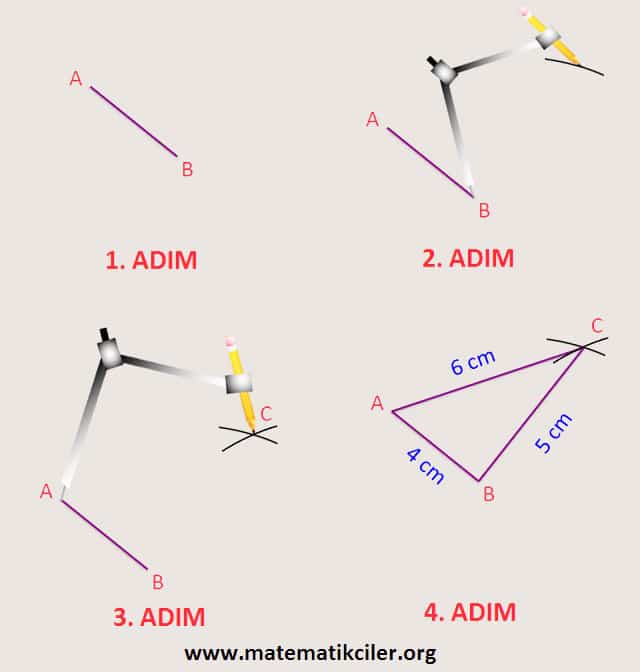
1) Üç Kenarının Uzunluğu Verilen Üçgenin Çizimi

Üç kenar uzunluğu verilen bir üçgen cetvel ve pergel kullanılarak çizilebilir.

ÖRNEK: Kenar uzunlukları 4 cm, 5 cm ve 6 cm olan üçgeni çizelim.

1. ADIM: Cetvel yardımıyla herhangi bir kenar çizilir.

4 cm uzunluğunda bir [AB] çizelim.

2. ADIM: Pergel, geriye kalan kenarlardan biri kadar açılır ve 1. adımda çizilen doğru parçasının bir ucuna konulur ve bir yay çizilir.

B noktasını merkez alarak pergelle 5 cm yarıçaplı bir yay çizelim.

3. ADIM: Bu sefer pergel son kalan kenarın uzunluğu kadar açılır ve 1. adımda çizilen doğru parçasının diğer ucuna koyup 2. adımda çizdiğimiz yayla kesişecek bir yay çizilir.

A noktasını merkez alarak pergelle 6 cm yarıçaplı bir yay çizelim. Bu yayın diğer yayla kesiştiği noktayı C olarak isimlendirelim.

4. ADIM: Bu yayların kesişim noktası, 1. adımda çizilen doğru parçasının uçları ile birleştirilerek üçgen oluşturulur.

Cetvel kullanarak C noktasını A ve B noktaları ile birleştirelim.

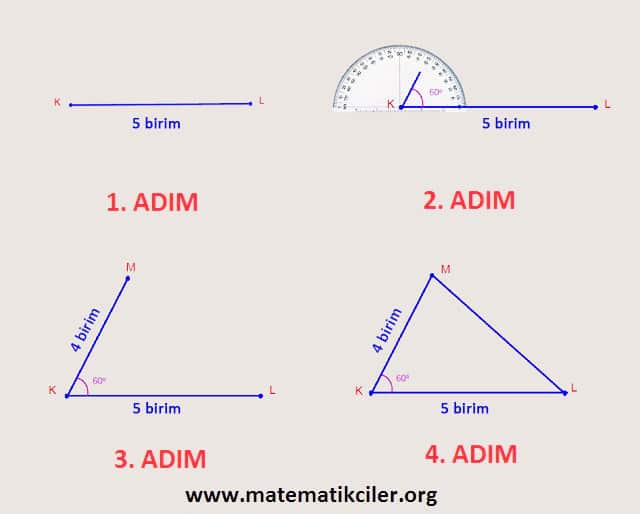
2) İki Kenarının Uzunluğu ve Bir Açısının Ölçüsü Verilen Üçgenin Çizimi

İki kenar uzunluğu ile bu kenarlar arasındaki açının ölçüsü verilen bir üçgen açıölçer ve cetvel yardımıyla çizilebilir.

ÖRNEK: |KL| = 5 birim, |KM| = 4 birim ve m(LKM)=60° olan bir KLM üçgeni çizelim.

1. ADIM: Cetvel yardımıyla verilen bir kenar çizilir.

5 birim uzunluğundaki [KL]’nı çizelim.

2. ADIM: Çizilen doğru parçasının ucuna verilen açı oluşturulur.

K noktasını merkez alarak açıölçerle ölçüsü 60° olan LKM açısını çizelim.

3. ADIM: Verilen diğer kenar, 1. adımda çizdiğimiz kenarın ucuna 2. adımda oluşturduğumuz açıyı yapacak şekilde çizilir.

Uzunluğu 4 birim olan [KM]’nı çizelim.

4. ADIM: Çizilen kenarların uçları birleştirerek üçgen oluşturulur.

M ve L noktalarını bir doğru parçasıyla birleştirelim ve KLM üçgenini elde edelim.

3) Bir Kenarının Uzunluğu ve İki Açısının Ölçüsü Verilen Üçgenin Çizimi

Bir kenarının uzunluğu ile bu kenara ait açılarının ölçüleri verilen bir üçgen açıölçer ve cetvel yardımıyla çizilebilir.

ÖRNEK: |DE| = 6 cm, m(DEF) = 45° ve m(EDF) = 55° olan bir DEF üçgeni çizelim.

1. ADIM: Cetvel yardımıyla verilen kenar çizilir.

6 cm uzunluğunda bir [DE] çizelim.

2. ADIM: Açı ölçer yardımıyla 1. adımdaki doğru parçasının bir ucuna, o köşe için verilen açıyı oluşturacak şekilde bir doğru parçası çizilir.

Açıölçeri kullanarak ölçüsü 45° olan DEF açısını oluşturalım.

3. ADIM: Açı ölçer yardımıyla 1. adımdaki doğru parçasının diğer ucuna, o köşe için verilen açıyı oluşturacak şekilde bir doğru parçası çizilir.

Benzer şekilde ölçüsü 55° olan EDF açısını oluşturalım.

4. ADIM: Çizdiğimiz bu kollar kesiştirilerek üçgen oluşturulur.

Bu iki açının kollarını üçgen oluşturacak şekilde uzatarak birleştirelim.

Sadece üç açısının ölçüsü verilen (herhangi bir kenar uzunluğu verilmeyen) belirli bir üçgen çizilemez. Bu bilgilerle sonsuz farklı üçgen çizilebilir.

ÖRNEK: Bütün açıları 60° olan bir üçgen çizelim. Bu üçgen eşkenar üçgendir ve her boyutta eşkenar üçgen çizebileceğimiz için belirli bir üçgen çizemeyiz.

KONUYU PEKİŞTİRMEK İÇİN: