Sayma Yöntemleri Konu Anlatımı

BİRE BİR EŞLEME YOLUYLA SAYMA

Bir kümenin eleman sayısını, verilen kümenin elemanları ile pozitif tam sayılar kümesinin elemanları arasında bire bir eşleme yaparak bulma işlemine bire bir eşleme yoluyla sayma denir.

ÖRNEK: İSTANBUL kelimesinin harflerinden oluşan kümenin eleman sayısını bire bir eşleme yoluyla bulalım.

İSTANBUL kelimesinin harflerinden oluşan kümeye H diyecek olursak H = { İ, S, T, A, N, B, U, L } olur.

Pozitif tam sayılar kümesi de Z⁺ = { 1, 2, 3, 4, 5, …} olduğuna göre bu iki kümenin elemanlarını eşleştirelim.

İ → 1
S → 2
T → 3
A → 4
N → 5
B → 6
U → 7
L → 8

Bire bir eşleme yolu ile H kümesinin eleman sayısının 8 olduğu bulunur. s(H) = 8

TOPLAMA YOLUYLA SAYMA

Sonlu ve ayrık kümelerin birleşiminin eleman sayısı bu kümelerin eleman sayıları toplamına eşittir. Bu yöntemle saymaya toplama yoluyla sayma denir.

A ile B sonlu ve ayrık iki küme olmak üzere s(A \(\cup\) B) = s(A) + s(B) olur.

ÖRNEK: İstanbul’un Anadolu yakasından Avrupa yakasına geçiş için 3 köprü ve 2 tünel bulunmaktadır. Anadolu yakasından Avrupa yakasına geçiş için kaç yol olduğunu bulalım.

Köprüler kümesi K = { k₁, k₂, k₃ }
Tüneller kümesi T = { t₁, t₂ }

Köprüler kümesi ile tüneller kümesinin ortak elemanı olmadığı için bu kümeler ayrık kümelerdir. O zaman toplama yoluyla toplam geçiş yolu sayısını bulabiliriz.

s(K \(\cup\) T) = s(K) + s(T)
s(K \(\cup\) T) = 3 + 2 = 5 buluruz.

ÖRNEK: 5 farklı pasta ve 6 farklı sütlü tatlı arasından 1 pasta veya 1 sütlü tatlı kaç farklı şekilde seçilir bulalım.

Pasta kümesine P dersek s(P) = 5, sütlü tatlı kümesine T dersek s(T) = 6 olur.

s(P \(\cup\) T) = s(P) + s(T)
s(P \(\cup\) T) = 5 + 6 = 11 buluruz.

ÖRNEK: 3 farklı kot pantolon, 4 farklı kumaş pantolon ve 2 farklı kadife pantolon arasından 1 pantolon seçecek olan Senem’in kaç farklı seçim yapabileceğini bulalım.

Kot pantolonların kümesine O dersek s(O) = 3, kumaş pantolonların kümesine Ş dersek s(Ş) = 4, kadife pantolonların kümesine A dersek s(A) = 2 olur.

s(O \(\cup\) Ş \(\cup\) A) = s(O) + s(Ş) + s(A)
s(O \(\cup\) Ş \(\cup\) A) = 3 + 4 + 2 = 9 buluruz.

ÇARPMA YOLUYLA SAYMA

A ve B boş kümeden farklı, ayrık iki küme olmak üzere AxB kümesinin eleman sayısını bulma işlemine çarpma yoluyla sayma denir. Bu yöntemle yapılan sayma işlemine saymanın temel ilkesi de denilir.

s(AxB) = s(A) . s(B) şeklinde hesaplanır.

ÖRNEK: A kentinden B kentine 2 farklı yolla, B kentinden C kentine 3 farklı yolla gidilebilmektedir. A kentinden C kentine B’ye uğramak koşuluyla kaç farklı yolla gidilebilir bulalım.

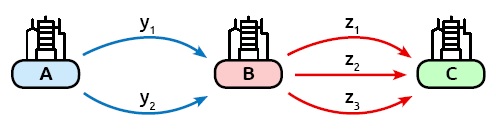
A kentinden B kentine giden yollara Y = {y₁, y₂},
B kentinden C kentine giden yollara Z = {z₁, z₂, z₃} diyelim.

A kentinden C kentine B’ye uğramak koşuluyla gidilebilecek yollar
YxZ = { (y₁,z₁), (y₁,z₂), (y₁,z₃), (y₂,z₁), (y₂,z₂), (y₂,z₃) } olur.

Bu kartezyen çarpım kümesinin eleman sayısı s(YxZ) = s(Y).s(Z) = 2.3 = 6 olarak bulunur.

ÖRNEK: 3 farklı yiyecek ve 4 farklı içecek arasından 1 yiyecek ve 1 içecek kaç farklı şekilde seçilir bulalım.

1. yiyecek 4 farklı içecekle, 2. yiyecek 4 farklı içecekle, 3. yiyecek de 4 farklı içecekle seçilebilir.

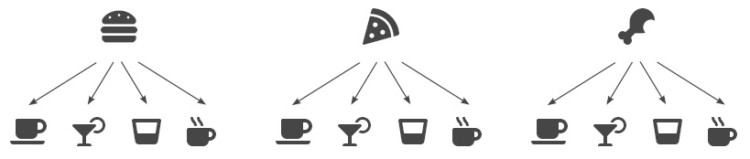
Kısaca yiyecek 3 şekilde, içecek 4 şekilde seçilebildiği için 1 yiyecek ve 1 içecek 3 . 4 = 12 farklı şekilde seçilebilir.

ÇÖZÜMLÜ ÖRNEK SORULAR

ÖRNEK 1: Alfabemizden 1 sesli veya 1 sessiz harf kaç farklı şekilde seçilebilir bulalım.

Alfabemizde 8 sesli, 21 sessiz harf vardır. Sesli veya sessiz fark etmeksizin 1 tane harf seçeceğimiz için bu seçim 8+21 = 29 farklı şekilde yapılabilir.

ÖRNEK 2: Alfabemizden 1 sesli ve 1 sessiz harf kaç farklı şekilde seçilebilir bulalım.

8 sesli harf arasından 1 tanesini ve 21 sessiz harf arasında 1 tanesini seçeceğiz. Bu seçim 8.21 = 168 farklı şekilde yapılabilir.

ÖRNEK 3: A şehrinden B şehrine 4 farklı yol, B şehrinden C şehrine 3 farklı yol vardır. Buna göre aşağıdaki soruları cevaplayalım.

3A) A şehrinden C şehrine, B şehrine uğramak koşuluyla kaç farklı şekilde gidilebilir?

A’dan B’ye 4 farklı yol, B’den C’ye 3 farklı yol vardı.
[A] → 4 → [B] → 3 → [C]
4.3 = 12

3B) A şehrinden C şehrine, giderken ve dönerken B şehrine uğramak koşuluyla kaç farklı şekilde gidip dönülebilir?

Dönüş yolunda C’den B’ye 3, B’den A’ya 4 yol vardır.
[A] → 4 → [B] → 3 → [C] → 3 → [B] → 4 → [A]
4.3.3.4 = 144

3C) A şehrinden C şehrine, giderken ve dönerken B şehrine uğramak ve giderken kullanılan yollar dönerken kullanılmamak koşuluyla kaç farklı şekilde gidip dönülebilir?

Dönüş yolunda C’den B’ye kullanılmayan 2, B’den A’ya kullanılmayan 3 yol vardır.
[A] → 4 → [B] → 3 → [C] → 2 → [B] → 3 → [A]
4.3.2.3 = 72

ÖRNEK 4: A = {1, 2, 3, 4, 5} olmak üzere, A kümesinin elemanları kullanılarak yazılabilecek sayılarla ilgili aşağıdaki soruları cevaplayalım.

4A) Üç basamaklı kaç farklı doğal sayı yazılabilir?

Basamak:	Yüzler	Onlar	Birler
Gelebilecek Rakamlar:	1, 2, 3, 4, 5	1, 2, 3, 4, 5	1, 2, 3, 4, 5
Rakam Sayısı:	5	5	5

5.5.5 = 125 farklı üç basamaklı doğal sayı yazılabilir.

4B) Üç basamaklı rakamları farklı kaç farklı doğal sayı yazılabilir?

Rakamları farklı olması için kullanılan rakam tekrar kullanılmamalıdır.

Basamak:	Yüzler	Onlar	Birler
Gelebilecek Rakamlar:	1, 2, 3, 4, 5	1, 2, 3, 4, 5 arasından biri kullanıldı	1, 2, 3, 4, 5 arasından ikisi kullanıldı
Rakam Sayısı:	5	4	3

5.4.3 = 60 tane rakamları farklı üç basamaklı doğal sayı yazılabilir.

4C) Üç basamaklı kaç farklı çift doğal sayı yazılabilir?

Basamak:	Yüzler	Onlar	Birler
Gelebilecek Rakamlar:	1, 2, 3, 4, 5	1, 2, 3, 4, 5	2,4
Rakam Sayısı:	5	5	2

5.5.2 = 50 farklı üç basamaklı çift doğal sayı yazılabilir.

4D) Üç basamaklı 200’den büyük kaç farklı doğal sayı yazılabilir?

Basamak:	Yüzler	Onlar	Birler
Gelebilecek Rakamlar:	2, 3, 4, 5	1, 2, 3, 4, 5	1, 2, 3, 4, 5
Rakam Sayısı:	4	5	5

4.5.5 = 100 farklı 200’den büyük üç basamaklı doğal sayı yazılabilir.

ÖRNEK 5: A = {0, 1, 2, 3, 4, 5} olmak üzere, A kümesinin elemanları kullanılarak yazılabilecek sayılarla ilgili aşağıdaki soruları cevaplayalım.

5A) Üç basamaklı kaç farklı doğal sayı yazılabilir?

Üç basamaklı sayı olabilmesi için 0 ile başlamaması gerekir.

Basamak:	Yüzler	Onlar	Birler
Gelebilecek Rakamlar:	1, 2, 3, 4, 5	0, 1, 2, 3, 4, 5	0, 1, 2, 3, 4, 5
Rakam Sayısı:	5	6	6

5.6.6 = 180 farklı üç basamaklı yazılabilir.

5B) Üç basamaklı rakamları farklı kaç farklı doğal sayı yazılabilir?

Rakamları farklı olması için kullanılan rakam tekrar kullanılmamalıdır.

Basamak:	Yüzler	Onlar	Birler
Gelebilecek Rakamlar:	1, 2, 3, 4, 5	0, 1, 2, 3, 4, 5 arasından biri kullanıldı	0, 1, 2, 3, 4, 5 arasından ikisi kullanıldı
Rakam Sayısı:	5	5	4

5.5.4 = 100 tane rakamları farklı üç basamaklı doğal sayı yazılabilir.

5C) Dört basamaklı rakamları farklı 5’e tam bölünebilen kaç farklı doğal sayı yazılabilir?

5’e bölünebilmesi için birler basamağı 0 veya 5 olmalıdır. Ayrıca dört basamaklı olabilmesi için 0 ile başlamaması gerekir. Bu yüzden bu soruyu öncelikle 0 ve 5’i birler basamağına ayrı ayrı sabitleyip çözeceğiz.

Basamak:	Binler	Yüzler	Onlar	Birler [0]
Rakam Sayısı:	5	4	3	1

Basamak:	Binler	Yüzler	Onlar	Birler [5]
Rakam Sayısı:	4	4	3	1

Birler basamağı 0 olan 5.4.3.1 = 60 tane, birler basamağı 5 olan 4.4.3.1 = 48 tane sayı yazılabilir. Toplam 60 + 48 = 108 tane rakamları farklı 5’e tam bölünebilen dört basamaklı doğal sayı yazılabilir.

ÖRNEK 6: 4 farklı mektup 5 farklı posta kutusuna kaç farklı şekilde atılabilir bulalım.

Mektup:	1.	2.	3.	4.
Atılabileceği Posta Kutusu Sayısı:	5	5	5	5

Bu 4 mektup 5.5.5.5 = 625 farklı şekilde posta kutularına atılabilir.

ÖRNEK 7: 5 farklı kuş 8 farklı dala her dalda en fazla bir kuş olmak şartıyla kaç farklı şekilde konabilir.

Bir kuşun konduğu dala başka bir kuş konamayacağı için dal seçeneği birer birer azalmaktadır.

Kuş:	1.	2.	3.	4.	5.
Konabileceği Dal Sayısı:	8	7	6	5	4

Bu kuşlar dallara 8.7.6.5.4 = 6720 farklı şekilde konabilir.

ÖNCEKİ KONU	SONRAKİ KONU
10. Sınıf Matematik Konuları	Faktöriyel

matematikciler.com olarak ziyaretçilerimize ücretsiz ve nitelikli içerikler sunmak için yoğun çaba sarfediyoruz. Bu emeğin korunması adına bu konu anlatımının izinsiz yayınlanması yasaktır!