Kesirleri Sıralama ve Sayı Doğrusunda Gösterme

BU KONUDA ÖĞRENECEKLERİMİZ:
√ Kesirlerin Karşılaştırılması
√ Kesirlerde Sıralama
√ Bütüne ve Yarıma Yakınlık

KESİRLERDE KARŞILAŞTIRMA VE SIRALANMA

Kesirlerde sıralama işlemi yaparken kesirleri birbirleri ile karşılaştırırız. Karşılaştırma ve sıralama işlemini küçüktür ( < ), büyüktür ( > ) ve eşittir ( = ) sembolleriyle yaparız.

Payları eşit olan kesirlerde sıralama, paydaları eşit olan kesirleri sıralama, tam sayılı kesirlerde sıralama, bir doğal sayı ile kesrin karşılaştırılması, yarıma yakınlığa bakarak karşılaştırma ve bütüne yakınlığa bakarak karşılaştırmayı görelim.

PAYLARI EŞİT OLAN KESİRLERİ SIRALAMA

Payları eşit olan kesirleri sıralamak için kesirlerin paydalarına bakarız. Paydası küçük olan kesir daha büyüktür.

ÖRNEK: \(\frac26\) ile \(\frac23\) kesirlerini karşılaştıralım.

\(\frac26\) kesri 6 eş parçaya ayrılmış bir bütünün 2 parçasını, \(\frac23\) kesri ise 3 eş parçaya ayrılmış bir bütünün 2 parçasını temsil etmektedir.

Bu yüzden bu kesirlerin sıralanışı:

\(\frac26<\frac23\) olur.

ÖRNEK: \(\frac{11}7\), \(\frac{11}{13}\) ve \(\frac{11}5\) kesirlerini küçükten büyüğe sıralayalım.

Kesirlerin payları eşit olduğu için paydası büyük olan daha küçüktür. Bu yüzden bu kesirlerin sıralanışı:

\(\frac{11}{13}<\frac{11}7<\frac{11}5\) olur.

PAYDALARI EŞİT OLAN KESİRLERİ SIRALAMA

Paydaları eşit olan kesirleri sıralamak için kesirlerin paylarına bakarız. Payı büyük olan kesir daha büyüktür.

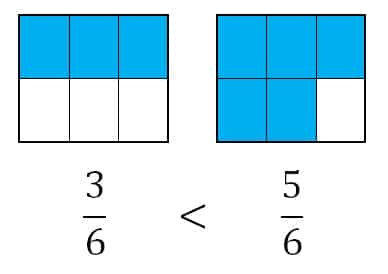
ÖRNEK: \(\frac36\) ile \(\frac56\) kesirlerini karşılaştıralım.

\(\frac36\) kesri 6 eş parçaya ayrılmış bir bütünün 3 parçasını, \(\frac56\) kesri ise 6 eş parçaya ayrılmış bir bütünün 5 parçasını temsil etmektedir.

Bu yüzden bu kesirlerin sıralanışı:

\(\frac36<\frac56\) olur.

ÖRNEK: \(\frac{15}{17}\), \(\frac8{17}\) ve \(\frac{11}{17}\) kesirlerini küçükten büyüğe sıralayalım.

Kesirlerin paydaları eşit olduğu için payı küçük olan daha küçüktür. Bu yüzden bu kesirlerin sıralanışı:

\(\frac8{17}<\frac{11}{17}<\frac{15}{17}\) olur.

PAYLARI VE PAYDALARI EŞİT OLMAYAN KESİRLERİ SIRALAMA

Payları ve paydaları eşit olmayan kesirleri sıralamak için öncelikle kesirlerde genişletme yaparak paylarını veya paydalarını eşitleriz. Paylarını veya paydalarını eşitlemekten hangisi kolay oluyorsa onu yapabiliriz. Eşitledikten sonra yukarıda gördüğümüz şekilde karşılaştırır ve sıralarız.

ÖRNEK: \(\frac75\) ile \(\frac{11}{15}\) kesirlerini karşılaştıralım.

Bu kesirlerin paydalarını eşitlemek, paylarını eşitlemekten daha kolaydır. Bu yüzden bu kesirlerin paydalarını eşitleriz ve karşılaştırırız:

\(\underset{(3)}{\frac75}=\frac{21}{15}\) olarak paydaları eşitleriz ve \(\frac{21}{15}>\frac{11}{15}\) olduğu için \(\frac75>\frac{11}{15}\) olur.

ÖRNEK: \(\frac3{17}\) ile \(\frac4{25}\) kesirlerini karşılaştıralım.

Bu kesirlerin paylarını eşitlemek, paydalarını eşitlemekten daha kolaydır. Bu yüzden bu kesirlerin paylarını eşitleriz ve karşılaştırırız:

\(\underset{(4)}{\frac3{17}}=\frac{12}{68}\) ve \(\underset{(3)}{\frac4{25}}=\frac{12}{75}\) olarak paydaları eşitleriz.

\(\frac{12}{68}>\frac{12}{75}\) olduğu için \(\frac3{17}>\frac4{25}\) olur.

TAM SAYILI KESİRLERİ SIRALAMA

Tam sayılı kesirleri karşılaştırırken iki yol izleyebiliriz.
1. YOL: Önce tam sayılı kesri bileşik kesre çevirme işlemi yaparız, daha sonra yukarıda öğrendiğimiz gibi paylarını veya paydalarını eşitleyerek karşılaştırırız.
2. YOL: Tam sayılı kesirlerde tam kısmı büyük olan kesir daha büyüktür. Eğer tam kısımları eşitse kesir kısımlarını karşılaştırırız. Kesir kısımlarını karşılaştırmayı da yukarıda öğrenmiştik.

BÜTÜNE YAKINLIK

Kesirlerin bütüne yakınlıklarına göre karşılaştırma yapabiliriz.

ÖRNEK:\(\frac45\) ve \(\frac78\) kesirlerini karşılaştıralım.

\(\frac45\) birden küçüktür ve bütüne (1’e) olan uzaklığı \(\frac15\)‘tir.

\(\frac78\) birden küçüktür ve bütüne (1’e) olan uzaklığı \(\frac18\)‘dir.

\(\frac18\) kesri \(\frac15\) ‘ten daha küçük bir kesir olduğu için \(\frac78\) kesrinin 1 tama olan mesafesi daha azdır. Yani daha yakındır.

Buradan \(\frac78\) > \(\frac45\) sıralamasını yapabiliriz.

ÖRNEK: \(\frac{11}5\) ve \(\frac{17}8\) kesirlerini karşılaştıralım.

\(\frac{11}5\) kesri 2 tamdan büyüktür ve 2 tamı \(\frac15\) geçmiştir.

\(\frac{17}8\) kesri 2 tamdan büyüktür ve 2 tamı \(\frac18\) geçmiştir.

\(\frac18\) kesri \(\frac15\)‘ten daha küçük bir kesir olduğu için \(\frac{17}8\)

kesri daha küçüktür. Çünkü iki kesir de 2 tamı geçmiştir. Ancak \(\frac{17}8\) kesri tamı \(\frac18\) geçmiştir, diğeri \(\frac15\) geçmiştir.

\(\frac18\) daha küçük olduğu için \(\frac{17}8\) daha az geçmiştir.

Buradan \(\frac{17}8\) < \(\frac{11}5\) sıralamasını yapabiliriz.

YARIMA YAKINLIK

Kesirlerin yarıma (\(\frac12\)‘ye) yakınlıklarına göre karşılaştırma yapabiliriz.

ÖRNEK: \(\frac9{20}\) ve \(\frac{11}{24}\) kesirlerini karşılaştıralım.

\(\frac9{20}\) kesri yarımdan ( \(\frac{10}{20}\) ) küçüktür ve yarıma olan uzaklığı \(\frac1{20}\)‘dir.

\(\frac{11}{24}\) kesri yarımdan ( \(\frac{12}{24}\) ) küçüktür ve yarıma olan uzak \(\frac1{24}\)‘tür.

\(\frac1{24}\) kesri \(\frac1{20}\)‘den daha küçük bir kesir olduğu için \(\frac{11}{24}\) kesrinin yarıma olan mesafesi daha azdır. Yani daha yakındır.

Buradan \(\frac{11}{24}\) > \(\frac9{20}\) sıralamasını yapabiliriz.

ÖRNEK: \(\frac{11}{20}\) ve \(\frac{17}{32}\) kesirlerini karşılaştıralım.

\(\frac{11}{20}\) kesri yarımdan (\(\frac{10}{20}\)) büyüktür ve yarımı \(\frac1{20}\) geçmiştir.

\(\frac{17}{32}\) kesri yarımdan (\(\frac{16}{32}\)) büyüktür ve yarımı \(\frac1{32}\) geçmiştir.

\(\frac1{32}\) kesri \(\frac1{20}\)‘den daha küçük bir kesir olduğu için \(\frac{17}{32}\) kesri daha küçüktür. Çünkü iki kesir de yarımı geçmiştir. Ancak \(\frac{17}{32}\) kesri yarımı daha az geçmiştir.

Buradan \(\frac{17}{32}\) < \(\frac{11}{20}\) sıralamasını yapabiliriz.

KESİRLERİ SAYI DOĞRUSUNDA GÖSTERME

BASİT KESİRLERİ SAYI DOĞRUSUNDA GÖSTERME

Basit kesirler sayı doğrusunda 0 ile 1 arasındadır. 0 ile 1 arası kesrin paydası kadar eş parçaya bölünür ve payı kadar parça ilerlenerek kesrin yeri bulunur.

ÖRNEK: \(\frac34\)kesrini sayı doğrusunda gösterelim.

Basit Kesirleri Sayı Doğrusunda Gösterme

BİLEŞİK VE TAM SAYILI KESİRLERİ SAYI DOĞRUSUNDA GÖSTERME

Bileşik kesirler önce tam sayılı kesre çevrilir. Kesir, tam kısmındaki sayı ve bir fazlası arasındadır. Bu aralık kesrin paydası kadar eş parçaya bölünür ve payı kadar parça ilerlenerek kesrin yeri bulunur.

ÖRNEK: \(\frac{13}5\) kesrini sayı doğrusunda gösterelim.

Bu kesir önce tam sayılı kesre çevrilir \(\frac{13}5=2\frac35\), daha sonra aşağıdaki gibi sayı doğrusunda gösterilir.

Bileşik Kesirleri Sayı Doğrusunda Gösterme

√ Kesirleri karşılaştırır, sıralar ve sayı doğrusunda gösterir.