Kümelerde Birleşim ve Kesişim

BU KONUDA ÖĞRENECEKLERİMİZ:
✓ Kümelerde Kesişim İşlemi
✓ Kümelerde Birleşim İşlemi

KESİŞİM KÜMESİ

A ve B gibi iki kümenin ortak elemanlarından oluşan kümeye A ile B’nin kesişim kümesi denir ve A  \(\cap\) B biçiminde gösterilir.

A ve B kümelerinin kesişim kümesi, Venn şeması ile aşağıdaki gibi gösterilir.

ÖRNEK: Aşağıdaki kümelerin kesişim kümelerini bulalım.

► A = { 1, 2, 3, 4 } ve B = { 3, 4, 5, 6, 7 }

“3” ve “4” her iki kümede de bulunduğu için bu iki eleman kesişim kümesini oluşturur.

A \(\cap\) B = { 3, 4 }

► K = { a, b, c } ve L = { k, l, m, n, p }

Bu iki kümede ortak eleman olmadığı için kesişim kümesi boş kümedir. Ortak elemanı olmayan kümelere ayrık kümeler de denilir.

K \(\cap\) L = { }

► P = { 1, 2, 3, 4 }, R = { 4, 5, 6 } ve S = { 2, 4, 6, 8 }

Bu üç kümenin kesişim kümesi bu üç kümede de yer alan “4” elemanından oluşur.

P \(\cap\) R \(\cap\) S = { 4 }

BİRLEŞİM KÜMESİ

A ve B gibi iki kümenin bütün elemanlarından oluşan kümeye A ile B’nin birleşim kümesi denir ve A  \(\cup\) B biçiminde gösterilir.

A ve B kümelerinin birleşim kümesi, Venn şeması ile aşağıdaki gibi gösterilir.

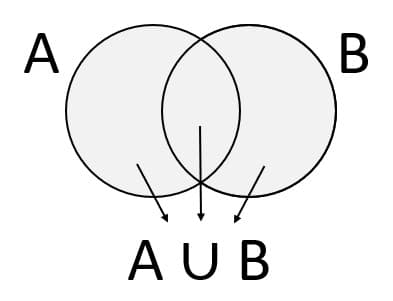
ÖRNEK: Aşağıdaki kümelerin birleşim kümelerini bulalım.

Birleşim kümesi yazılırken kümelerdeki bütün elemanlar sadece bir kez yazılır.

► A = { 1, 2, 3, 4 } ve B = { 3, 4, 5, 6, 7 }

A \(\cup\) B = { 1, 2, 3, 4, 5, 6, 7 }

► C = { a, b, c } ve D = { k, l, m }

C \(\cup\) D = { a, b, c, k, l, m }

► P = { 1, 2, 3, 4 }, R = { 4, 5, 6 } ve S = { 2, 4, 6, 8 }

P \(\cup\) R \(\cup\) S = { 1, 2, 3, 4, 5, 6, 8 }

ÖRNEK: Aşağıdaki kümelerin kesişim ve birleşim kümelerini bulalım.

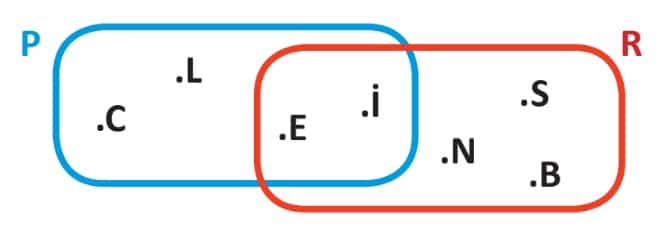
P \(\cap\) R = { E, İ }

P \(\cup\) R = { C, L, E, İ, N, S, B }

KONUYU PEKİŞTİRMEK İÇİN: