- BU KONUDA ÖĞRENECEKLERİMİZ:
- √ Histogram Nedir?
- √ Histogram Oluşturma
- √ Histogram Yorumlama
HİSTOGRAM NEDİR?
Gruplandırılmış bir veri dağılımının sütun grafiğiyle gösterimine histogram adı verilir. Diğer bir ifadeyle tekrarlı sayılardan oluşan elimizdeki verileri, uygulanan işlemlerden sonra önce tabloya, tablodan yararlanarak grafiğe aktarılması yani veri gruplarının grafiğinin dikdörtgen sütunlar halinde gösterilmesine histogram denir.
HİSTOGRAM NASIL HAZIRLANIR?
Histogram oluşturmak için şu adımlar takip edilir:
1) Öncelikler veriler küçükten büyüğe sıralanır. (İşlemlerde kolaylık sağlar.)
2) Veri grubunun açıklığı (aralığı) bulunur. Açıklık en büyük veriden en küçük verinin çıkartılması ile elde edilir.
3) Verilerin kaç gruba ayrılacağı belirlenir. Veri gruplarının sayısının 10 civarında olması uygundur.
4) Grup genişliği bulunur. Açıklık değerinin grup sayısına bölünmesiyle elde edilen sayıdan büyük en küçük doğal sayı grup genişliği olarak alınır.
(Veri gruplarının sayısının 10 alınması hesaplamayı kolaylaştırır.)
5) Veriler en küçük veriden başlayarak grup genişliğine göre gruplara ayrılır.
6) Oluşturulan gruplar ve gruplardaki veri sayıları tablo halinde düzenlenir.
7) Tabloya bakılarak histogram çizilir.
HİSTOGRAM ÖRNEKLERİ
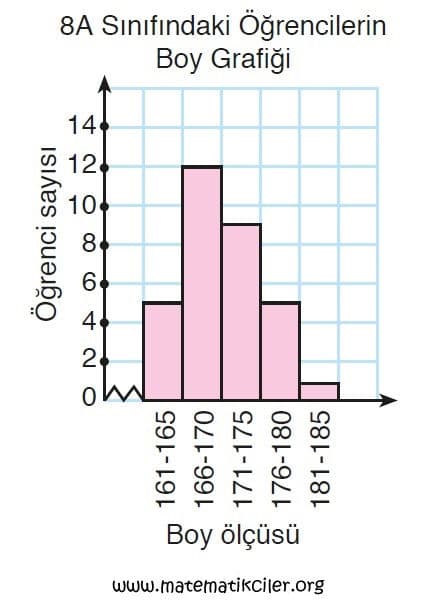
ÖRNEK: 8A sınıfındaki 32 öğrencinin boyları aşağıda verilmiştir. Bu verileri histogramla gösterelim.
Veriler: 162, 161, 170, 167, 170, 173, 163, 176, 174, 180, 179, 164, 169, 175, 177, 185, 169, 172, 180, 175, 168, 163, 172, 172, 169, 173, 170, 171, 168, 166, 167, 170.
1) Öncelikleri veriler küçükten büyüğe sıraladık.
161, 162, 163, 163, 164, 166, 167, 167, 168, 168, 169, 169, 169, 170, 170, 170, 170, 171, 172, 172, 172, 173, 173, 174, 175, 175, 176, 177, 179, 180, 180, 185
2) Veri grubunun açıklığını bulduk.
185 – 161 = 24
3) Verilerin kaç gruba ayrılacağı belirledik.
Grup sayımız 5 olsun
4) Grup genişliğini bulduk.
24 : 5 = 4,8 olup bu sayıdan büyük en küçük doğal sayı 5’tir.
5) Verileri grup genişliğine göre gruplara ayırdık.
Verilerdeki en küçük sayıdan başlayarak grup genişliği kadar sayı ilerleyerek bir grup yapıyoruz. Buradaki sayıların veriler arasında olma zorunluluğu yok.
161-162-163-164-165 gibi 5 tane veriyi 161-165 şeklinde yazıyoruz. O halde gruplarımız:
161-165 , 166-170 , 171-175 , 176-180 , 181-185
6) Gruplarımızı ve o gruplardaki veri sayılarını tablo halinde düzenledik.
| GRUPLAR | KİŞİ SAYISI |
| 161-165 | 5 |
| 166-170 | 12 |
| 171-175 | 9 |
| 176-180 | 5 |
| 181-185 | 1 |
7) Tabloya bakarak histogram çizdik.
 Histogram oluştururken dikkat edilmesi gereken noktalar:
Histogram oluştururken dikkat edilmesi gereken noktalar:
# Bir eksene gruplar (genelde yatay eksene) diğer eksene ise (genelde dikey eksene) gruptaki veriler yazılır.
# Eksen başlıkları yazılmalıdır. (Boy ölçüsü – Öğrenci sayısı)
# Grafiğin ölçeği uygun seçilmelidir. (0-2-4-6-… uygun bir seçim olmuş)
# Grafiğin adı unutulmamalıdır. (8A Sınıfındaki Öğrencilerin Boy Grafiği)
# 0-160 aralığında veri olmadığı için grafiği çizerken bu bölümü zikzaklı çizilir.
HİSTOGRAM NASIL YORUMLANIR?
Histogram yorumlama konusunu bir örnekle açıklayalım.

Yukarıdaki histograma göre aşağıdaki soruları cevaplandıralım.
1) Grup sayısı nedir?
Histogramdaki sütun sayısı grup sayısıdır. (21-30, 31-40 vb..) Bu histogramda 8 grup vardır.
2) Grup genişliği nedir?
İki yolla bulabiliriz. Birinci yol olarak bir gruptaki sınırları birbirinden çıkartırız ve 1 ekleriz.
Mesela gruplardan biri 81-90 olduğu için (90 – 81) + 1 = 9 + 1 = 10
İkinci yol olarak ardışık iki grubun aynı sınırları çıkartılır.
Örneğin:
41-50
51-60 gibi iki ardışık gruptaki büyük sayıları (veya küçük) birbirinden çıkartırız.
60-50 = 10
3) Açıklık en fazla kaç olabilir?
Verilerin gruplar içindeki dağılımı grafiğe bakarak anlaşılamayacağı için açıklık ve veriler konusunda farklı sorular sorulabilir.
Bu soruda 91-100 grubunda 1 öğrencinin var olduğunu biliyoruz ama bu öğrencinin kaç aldığını bilmiyoruz. En küçük veri 21’dir. Bu yüzden açıklık en fazla 100-21 = 79 olur.
4) Açıklık en az kaç olabilir?
En küçük veri 21’dir.(Çünkü grupları oluşturmaya en küçük veriden başlarız.) Yukarıda anlattığımız sebeplerden dolayı açıklık en az 91 – 21 = 70 olur.
5) Açıklık kaç olabilir?
70’ten 79’a kadar tüm değerler olabilir.
6) Notu 85’ten fazla kaç öğrenci olabilir?
Yine yukarıdaki mantığa göre:
91-100 aralığındaki 1 kişi
81-90 grubundaki 2 öğrenciyi de 85’ten yüksek aldığını düşünürsek en fazla 3 öğrenci eder.
KONU KAZANIMLARI
- √ Bir veri grubuna ilişkin histogram oluşturur ve yorumlar.
