BU KONUDA ÖĞRENECEKLERİMİZ:
✓ Pisagor teoremi ile ilgili problemler nasıl çözülür?
Pisagor bağıntısını öğrendikten sonra sıra geldi bu bilgilerimizi problem çözmede kullanmaya. Pisagor bağıntısı ile ilgili problemlere geçmeden önce Pisagor bağıntısı konu anlatımına göz atmanızda fayda var: Pisagor Bağıntısı
PROBLEM-1

Uzunluğu 25 m olan bir direk, yıldırım düşmesi nedeniyle şekildeki gibi kırılıyor. Son durumda direğin uç noktası direkten ne kadar uzakta olur?
ÇÖZÜM: II. durumda oluşan üçgeni çizelim. Direğin tamamının boyu 25 metredir ve 8 metrelik kısmı dik olarak kaldığı için geriye kalan 17 metrelik kısmı hipotenüsü oluşturur. Soruda bizde bu dik üçgenin verilmeyen kenarının uzunluğu sorulmaktadır. Bu uzunluk pisagor bağıntısı ile bulunabilir.
\(\begin{array}{l}8^2\;+\;x^2\;=\;17^2\\64\;+\;x^2\;=\;289\\x^2\;=\;289\;-\;64\\x^2\;=\;225\\\sqrt{x^2}\;=\;\sqrt{225}\\x\;=\;15\end{array}\)PROBLEM-2
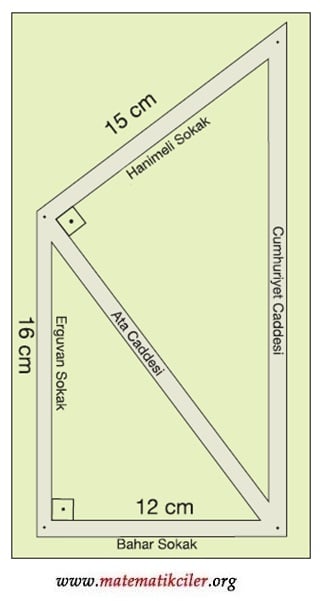
Bir mahallenin krokisinin bir kısmı yandaki şekilde verilmiştir. Verilenlere göre Cumhuriyet Caddesi’nin kroki üzerindeki uzunluğu kaç cm olur?
ÇÖZÜM: Soruda iki tane dik üçgen bulunmaktadır. Cumhuriyet Caddesi’nin uzunluğunu bulmak için Ata Caddesi’nin uzunluğunu bulmamız gerekiyor. Pisagor bağıntısını kullanarak Ata Caddesi’nin uzunluğu şu şekilde bulunur:
\(\begin{array}{l}12^2\;+\;16^2\;=\;a^2\\144\;+\;256\;=\;a^2\\400\;=\;a^2\\\sqrt{400}\;=\;\sqrt{a^2}\\20\;=\;a\end{array}\)Şimdi Cumhuriyet Caddesi’nin uzunluğunu diğer üçgende Pisagor bağıntısını kullanarak bulabiliriz.
\(\begin{array}{l}15^2\;+\;20^2\;=\;c^2,\\225\;+\;400\;=\;c^2\\625\;=\;c^2\\\sqrt{625}\;=\;\sqrt{c^2}\\25\;=\;c\end{array}\)Cumhuriyet Caddesinin krokideki boyunun 25 cm olduğunu bulduk.
PROBLEM-3
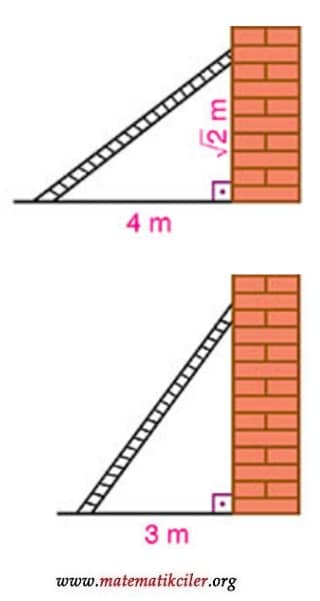
Yere dik olan duvara bir merdiven resimdeki gibi iki farklı şekilde yaslanıyor. Merdivenin alt ucu ile duvar arasındaki mesafe 4 m iken üst ucu yerden \(\sqrt2\)m yukarıda olduğuna göre, alt ucu ile duvar arasındaki mesafe 3 m iken üst ucunun yerden yüksekliği kaç metre olur?
ÇÖZÜM: İki durumda da dik üçgen oluşmuştur. Birinci durumdan merdivenin uzunluğunu (m diyelim) bulup ikinci durumdan yüksekliği (y diyelim) bulabiliriz. Bu yüzden önce 1. durumdaki üçgende Pisagor bağıntısı uygularız:
\(\begin{array}{l}4^2\;+\;\left(\sqrt2\right)^2\;=\;m^2\\16\;+\;2\;=\;m^2\\18\;=\;m^2\\\sqrt{18}\;=\;m\end{array}\)Merdivenin uzunluğunu bulduk. İkinci durumdaki merdiven aynı merdiven olduğu için burada Pisagor teoremi uygulayarak merdiven ucunun yerden yüksekliğini bulabiliriz:
\(\begin{array}{l}3^2\;+\;y^2\;=\;\left(\sqrt{18}\right)^2\\9\;+\;y^2\;=\;18\\y^2\;=\;9\\\sqrt{y^2}\;=\;\sqrt9\\y\;=\;3\end{array}\)Merdivenin ucunun 2. durumda yerden yüksekliğini 3 metre olarak bulduk.
KONUYU PEKİŞTİRMEK İÇİN:
İLGİLİ ÇALIŞMA KAĞIDI BAĞLANTISI
İLGİLİ KAZANIM TESTİ BAĞLANTISI
TEST ÇÖZME BAĞLANTISI
KONU KAZANIMLARI
BU KONUYLA İLGİLİ KAZANIMLAR:
✓ Pisagor bağıntısını oluşturur; ilgili problemleri çözer.
| ÖNCEKİ KONU | SONRAKİ KONU |
| Pisagor Teoremi (Pisagor Bağıntısı) | Üçgenlerde Eşlik ve Benzerlik |
