Trigonometri (Dik Üçgenlerdeki Trigonometrik Oranlar)

TRİGONOMETRİ NEDİR? NE İŞE YARAR?

Trigonometri kelimesi Yunanca trigōnon (üçgen) ve metron (ölçmek) kelimelerinin birleşmesiyle oluşmuştur. Trigonometri, üçgenlerin açıları ile kenarları arasındaki bağıntıları konu edinen bir matematik dalıdır. Trigonometri günümüzde ekonomi, fizik ve mühendislik alanlarında sıkça kullanılmaktadır.

DİK ÜÇGENDEKİ ORANLAR

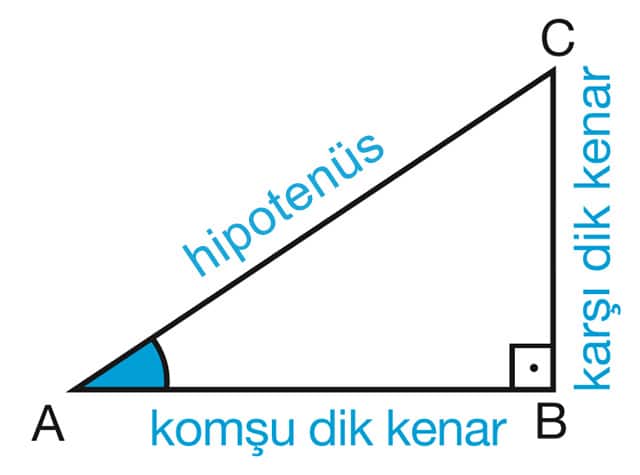Dik üçgende 90 derece dışındaki diğer açılardan birini seçelim. Örneğin resimde A açısı seçilmiştir.
Trigonometrik oranları yazarken resimdeki gibi bir isimlendirme kullanacağız. 90 derecenin karşısındaki kenara hipotenüs, seçtiğimiz açının karşısındaki kenara karşı kenar, geriye kalan ve açının bir kolu olan kenara ise komşu kenar diyeceğiz. İsimlendirme işinde de anlaştığımıza göre gelelim bu kenarları oranlamaya.

SİNÜS

Bir dik üçgende, bir dar açının karşısındaki dik kenar uzunluğunun hipotenüsün uzunluğuna oranına o dar açının sinüsü denir. Bir A açısının sinüsü “sin A” şeklinde gösterilir.

KOSİNÜS

Bir dik üçgende, bir dar açının komşu dik kenar uzunluğunun hipotenüsün uzunluğuna oranına o dar açının kosinüsü denir. Bir A açısının kosinüsü “cos A” şeklinde gösterilir.

TANJANT

Bir dik üçgende, bir dar açının karşısındaki dik kenar uzunluğunun komşu dik kenar uzunluğuna oranına o dar açının tanjantı denir. Bir A açısının tanjantı “tan A” şeklinde gösterilir.

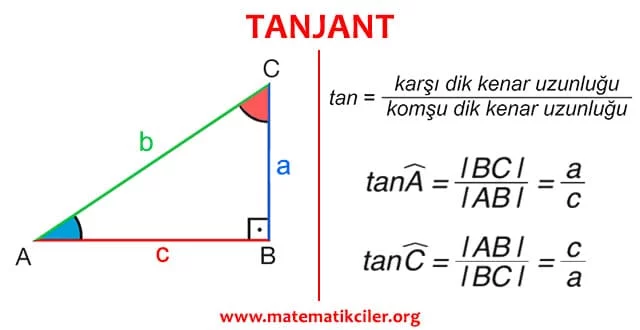
KOTANJANT

Bir dik üçgende, bir dar açının komşu dik kenar uzunluğunun karşısındaki dik kenar uzunluğuna oranına o dar açının kotanjantı denir. Bir A açısının kontanjantı “cot A” şeklinde gösterilir.

 ÇIKARILACAK DERSLER

Yukarıdaki trigonometrik oranları incelediğinizde aşağıdaki yazılanların bazılarını (belki hepsini) keşfetmiş olabilirsiniz. Ama biz yine de yazalım.
# Birbirini 90 dereceye tamamlayan (birbirinin tümleri olan) iki açıdan birinin sinüsü, diğerinin kosinüsüne eşittir.
# Birbirini 90 dereceye tamamlayan (birbirinin tümleri olan) iki açıdan birinin tanjantı, diğerinin kotanjantına eşittir.
# Bir dar açının tanjantı ile kotanjantı birbirinin çarpmaya göre tersidir. (Çarpmaya göre tersi?)
“Komşu/Hipotenüs Sinüs müydü, Kosinüs müydü?” veya “Komşu / Karşı Tanjant mıydı, Kotanjant mıydı?” gibi sorulara çözüm olarak şöyle bir yöntem izleyebilirsiniz. “Ko” ile başlayanların (yani kosinüs ve kotanjant) payında komşu var.

ÖZEL DİK ÜÇGENLERDE TRİGONOMETRİK ORANLAR

30 – 60 – 90 ÜÇGENİ

Eşkenar üçgende bir kenara ait yükseklik çizilirse oluşan iki dik üçgenin de açıları 30° – 60° – 90° olur. Bu eşkenar üçgenin bir kenarının uzunluğunu 2a kabul edersek, oluşan dik üçgenlerde 30 derecelik açının karşısı a olur çünkü yükseklik aynı zamanda kenarortaydır. Yüksekliğin uzunluğunu da Pisagor Bağıntısından bulabiliriz. Bu kenarları oranlarsak aşağıdaki trigonometrik oranları elde ederiz.

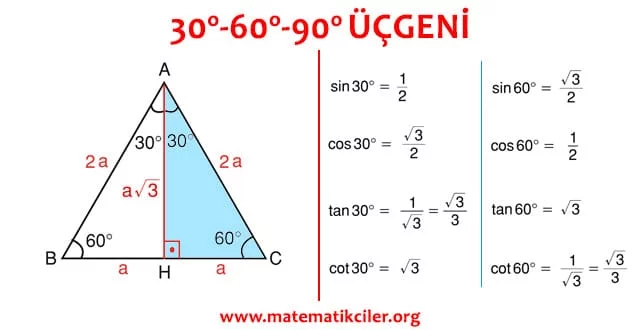
Buradan şu sonuçlara da varabiliriz. 30-60-90 üçgeninde:
# Hipotenüsün uzunluğu 30 derecelik açının karşısındaki kenarın uzunluğunun 2 katıdır.
# 60 derecelik açının karşısındaki kenarın uzunluğu, 30 derecelik açının karşısındaki kenarın uzunluğunun \(\sqrt3\) katıdır.

45- 45 – 90 ÜÇGENİ

İkizkenar bir dik üçgenin açıları 45° – 45° – 90° ‘dir. Bu ikizkenar dik üçgenin dik kenarlarının uzunluğunu a kabul edersek hipotenüsün uzunluğunu Pisagor Bağıntısından \(a\sqrt2\) buluruz. Bu kenarları oranlarsak aşağıdaki trigonometrik oranları elde ederiz.

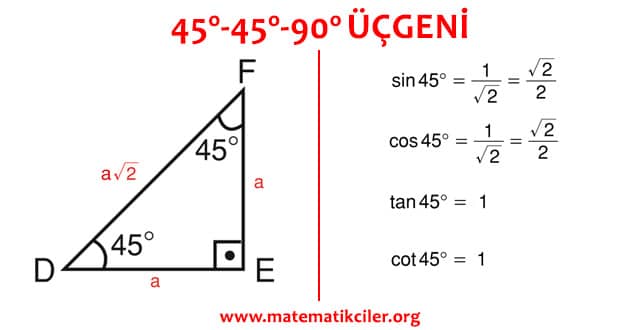
Buradan şu sonuca da varabiliriz. 45-45-90 üçgeninde:
# Hipotenüsün uzunluğu diğer kenarların uzunluğunun \(\sqrt2\) katıdır.

30° – 45° – 60° AÇILARININ TRİGONOMETRİK ORAN TABLOSU