Üçgenlerde Benzerlik Problemleri

BU KONUDA ÖĞRENECEKLERİMİZ:
✓ Üçgenlerde Benzerlik Problemleri nasıl çözülür?

Üçgenlerde eşlik ve benzerlik konusundan sonra öğrendiğimiz bu bilgileri problem çözmede kullanalım. Bu konuya geçmeden önce eşlik benzerlik konusunu tekrar etmenizde fayda var: Üçgenlerde Eşlik ve Benzerlik

PROBLEM-1

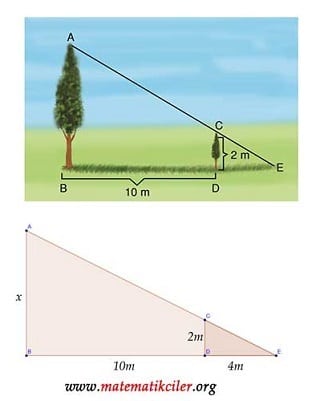
Resimdeki büyük ve küçük ağaçların gölgelerinin bitim noktaları aynıdır. İki ağaç arasındaki uzaklık 10 m, küçük ağacın gölgesi 4 m ve küçük ağacın boyu 2 m ise büyük ağacın boyu kaç metredir?

ÇÖZÜM:  Şekilde oluşan üçgenleri çizersek, bu üçgenlerin Açı Açı benzerlik şartını sağladığını görürüz ve benzerlik oranlarını şu şekilde yazarız: \(\begin{array}{l}\frac{\left|ED\right|}{\left|EB\right|}=\frac{\left|CD\right|}{\left|AB\right|}\\\frac4{14}=\frac2x\end{array}\)

İçler-dışlar çarpımı yaparız ve x’in değerini buluruz.

\(\begin{array}{l}\;4.x=2.14\\\;\;4x=28\\\;\;\;\;x=7\;m\end{array}\)

 PROBLEM-2

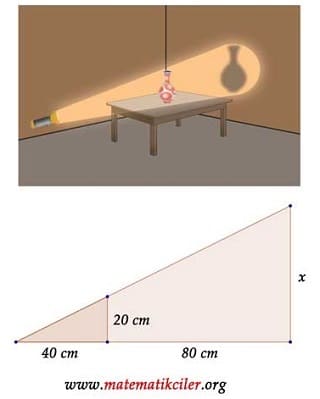
Sehpanın üzerinde duran 20 cm boyundaki bir vazoya 40 cm uzaklıktan, karanlık bir ortamda ışık tutuluyor. 80 cm uzaklıktaki duvarda oluşan vazonun gölgesi kaç santimetre boyundadır?

ÇÖZÜM:  Şekilde oluşan üçgenleri çizersek, bu üçgenlerin Açı Açı benzerlik şartını sağladığını görürüz ve benzerlik oranlarını şu şekilde yazarız: \(\frac{20}{40}=\frac x{120}\)

İçler-dışlar çarpımı yaparız ve x’in değerini buluruz.

\(\begin{array}{l}\;40.x=20.120\\\;\;40x=2400\\\;\;\;\;\;\;x=60\;cm\end{array}\)

PROBLEM-3

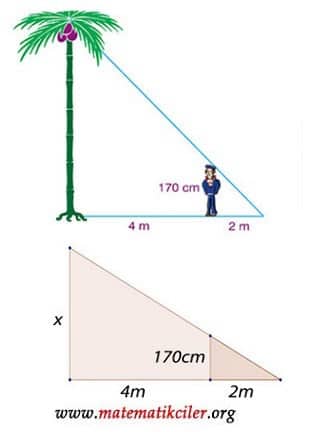
Resimde verilen kişinin boyu 170 cm olduğuna göre ağacın boyu kaç cm’dir?

ÇÖZÜM:  Şekilde oluşan üçgenleri çizersek, bu üçgenlerin Açı Açı benzerlik şartını sağladığını görürüz ve benzerlik oranlarını şu şekilde yazarız: \(\frac26=\frac{170}x\)

İçler-dışlar çarpımı yaparız ve x’in değerini buluruz.

\(\begin{array}{l}\;\;2.x=170.6\\\;\;\;2x=1020\\\;\;\;\;\;x=510\;cm\end{array}\)

KONUYU PEKİŞTİRMEK İÇİN:

ÖNCEKİ KONU	SONRAKİ KONU
Üçgenlerde Eşlik ve Benzerlik	Dönüşüm Geometrisi (Yansıma – Öteleme – Dönme)