Birinci Dereceden İki Bilinmeyenli Eşitsizlikler

TANIM VE KAVRAMLAR

> (büyüktür), ≥ (büyüktür veya eşittir), < (küçüktür), ≤ (küçüktür veya eşittir) sembolleri ile yazılan matematiksel ifadelere eşitsizlik denir.

a,b,c \(\in\) R ve a,b \(\neq\) 0 olmak üzere;

ax + by + c > 0
ax + by + c ≥ 0
ax + by + c < 0
ax + by + c ≤ 0

şeklindeki eşitsizliklere x ve y değişkenine bağlı birinci dereceden iki bilinmeyenli eşitsizlik denir.

Bir eşitsizliğin birinci dereceden iki bilinmeyenli eşitsizlik olabilmesi için iki değişken içermesi ve değişkenlerin kuvvetinin 1 olması gerekir.

► 3x + y > 6 ve y − 3x ≤ 5 eşitsizlikleri birinci dereceden iki bilinmeyenli eşitsizliklerdir.

Birinci dereceden iki bilinmeyenli eşitsizlikleri sağlayan x ve y gerçek sayıları (x, y) sıralı ikilisi olarak yazılır. Bu sıralı ikililerden her biri eşitsizliğin çözüm kümesinin bir elemanıdır.

ÖRNEK: x + y ≥ 3 eşitsizliğini sağlayan (x, y) sıralı ikililerini bulalım.

3 + 0 ≥ 3 doğru olur: (3, 0)

1 + 5 ≥ 3 doğru olur: (1, 5)

7 + 9 ≥ 3 doğru olur: (7, 9)

şeklinde sonsuz sıralı ikili bulabiliriz.

BİRİNCİ DERECEDEN İKİ BİLİNMEYENLİ EŞİTSİZLİKLERİN GRAFİKLERİ

Birinci dereceden iki bilinmeyenli eşitsizliklerin grafikleri koordinat sisteminde bir bölge belirtir. Bu bölge, eşitsizliği sağlayan (x, y) sıralı ikililerinin temsil ettiği noktalardan oluşur.

Eşitsizlik Grafiği Nasıl Çizilir?

1.ADIM:  Bir eşitsizliğin grafiğinin çizilebilmesi için öncelikle bu eşitsizliğin bölgesini sınırlayan doğrunun çizilmesi gerekir. Bunun için iki bilinmeyenli denklemler konusuna göz atabilirsiniz. Bu doğru koordinat sistemini iki bölgeye ayırır.

2. ADIM: Eşitsizlik ” < ” ya da ” > ”  sembolünü içeriyorsa sınır doğrumuz çözüm kümesine dahil değildir. Bu durumda sınır doğrusu kesikli çizgilerle gösterilir. Eğer eşitsizlik ” ≤ ” ya da ” ≥ ”  sembolünü içeriyorsa sınır doğrumuz çözüm kümesine dahildir. Bu durumda sınır doğrusu kesiksiz düz çizgiyle gösterilir.

3. ADIM: Doğrunun ayırdığı iki bölgeden biri eşitsizliğin çözüm kümesidir. Doğru bölgeyi belirlemek için sınır doğrusunun herhangi bir tarafından herhangi bir nokta seçilir. Seçilen bu noktanın koordinatları eşitsizlikte değişkenlere yazılır. Elde eşitsizlik doğru ise seçtiğimiz nokta çözüm kümesindedir, yanlış ise seçtiğimiz nokta çözüm kümesinde değildir. Bu bilgiye göre çözüm kümesi taranır.

ÖRNEK: 2x − 3y < 6 eşitsizliğinin grafiğini çizelim.

İlk olarak sınır doğrusunun (2x − 3y = 6) grafiği çizilir. Eşitsizliğimiz < sembolü içerdiği için sınır doğrusu kesikli çizilir.

Daha sonra hangi tarafın çözüm kümesi olduğunu belirlemek için rastgele bir nokta seçilir. Biz kolaylık olması için orijini (0, 0) tercih ettik. Eşitsizlikteki x ve y yerine 0 yazılır ve 0 < 6 elde edilir.

Doğru bir ifade elde ettiğimiz için (0, 0) noktası çözüm kümemizdedir yani taralı bölgededir.

ÖRNEK: y ≥ −2x eşitsizliğinin grafiğini çizelim.

İlk olarak sınır doğrusunun (y = −2x) grafiği çizilir. Eşitsizliğimiz ≥ sembolü içerdiği için sınır doğrusu kesiksiz düz çizilir.

Daha sonra hangi tarafın çözüm kümesi olduğunu belirlemek için rastgele bir nokta seçilir. Biz  (−3, −4) noktasını tercih ettik. Eşitsizlikteki x yerine −3, y yerine −4 yazılır ve −4 ≥ 6 elde edilir.

Yanlış bir ifade elde ettiğimiz için (−3, −4) noktası çözüm kümemizde değildir yani taralı bölgede değildir.

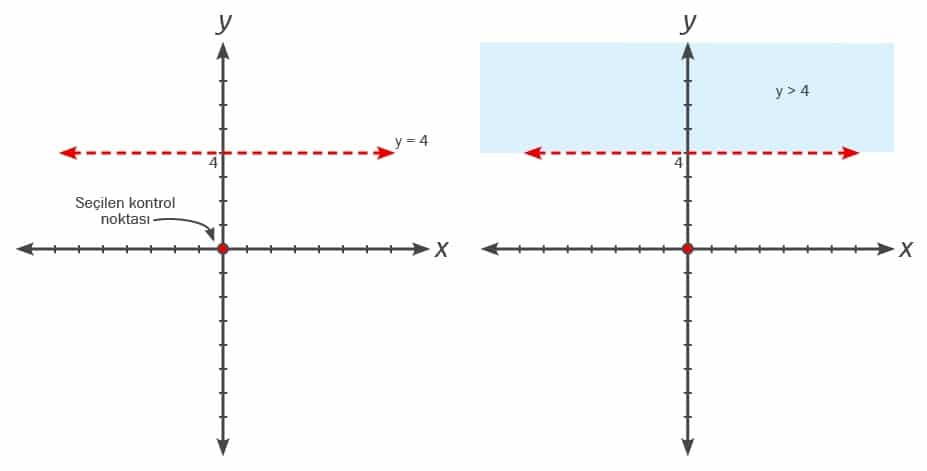
ÖRNEK: y > 4 eşitsizliğinin grafiğini çizelim.

İlk olarak sınır doğrusunun (y = 4) grafiği çizilir. Eşitsizliğimiz > sembolü içerdiği için sınır doğrusu kesikli çizilir.

Daha sonra hangi tarafın çözüm kümesi olduğunu belirlemek için rastgele bir nokta seçilir. Biz kolaylık olması için orijini (0, 0) tercih ettik. Eşitsizlikteki y yerine 0 yazılır ve 0 > 4 elde edilir.

Yanlış bir ifade elde ettiğimiz için (0, 0) noktası çözüm kümemizde değildir yani taralı bölgede değildir.

ÖRNEK: x ≤ −4 eşitsizliğinin grafiğini çizelim.

İlk olarak sınır doğrusunun (x = −4) grafiği çizilir. Eşitsizliğimiz ≤ sembolü içerdiği için sınır doğrusu kesiksiz düz çizilir.

Daha sonra hangi tarafın çözüm kümesi olduğunu belirlemek için rastgele bir nokta seçilir. Biz kolaylık olması için orijini (0, 0) tercih ettik. Eşitsizlikteki x yerine 0 yazılır ve 0 ≤ −4 elde edilir.

Yanlış bir ifade elde ettiğimiz için (0, 0) noktası çözüm kümemizde değildir yani taralı bölgede değildir.

EŞİTSİZLİK SİSTEMLERİ

En az iki tane birinci dereceden iki bilinmeyenli eşitsizliğin oluşturduğu sisteme birinci dereceden iki bilinmeyenli eşitsizlik sistemi denir. Her iki eşitsizliği de sağlayan (x, y) sıralı ikililerinin kümesine eşitsizlik sisteminin çözüm kümesi denir.

Birinci dereceden iki bilinmeyenli eşitsizliklerin grafikleri koordinat sisteminde bölge belirttikleri için eşitsizlik sisteminin çözüm kümesi bu bölgelerin kesişimidir.

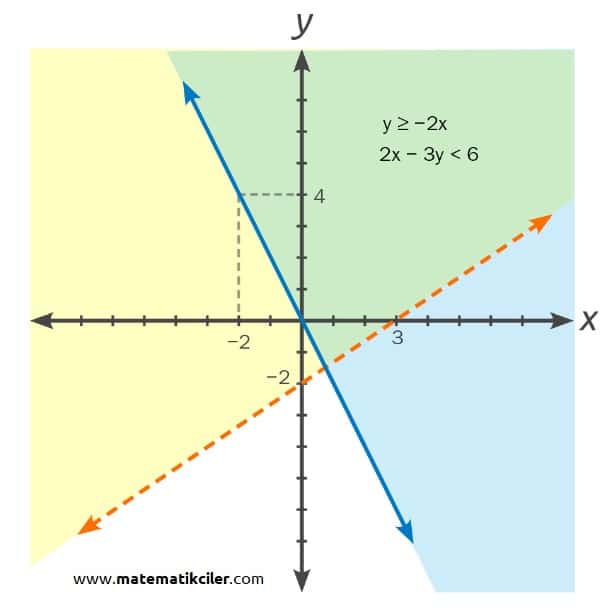
ÖRNEK: Aşağıdaki eşitsizlik sisteminin çözüm kümesini analitik düzlemde gösterelim.
y ≥ −2x
2x − 3y < 6

y ≥ −2x eşitsizliğinin çözüm kümesi mavi bölge ile gösterilmiştir. 2x − 3y < 6 eşitsizliğinin çözüm kümesi ise sarı bölge ile gösterilmiştir. Bu iki bölgenin kesişimi ( Sarı \(\cap\) Mavi = Yeşil) eşitsizlik sisteminin çözüm kümesidir.

matematikciler.com olarak ziyaretçilerimize ücretsiz ve nitelikli içerikler sunmak için yoğun çaba sarfediyoruz. Bu emeğin korunması adına bu konu anlatımının izinsiz yayınlanması yasaktır!