Fonksiyon Kavramı

Fonksiyon konusu için günlük hayatta sıklıkla karşılaşılan dönüşüm işleminin matematiksel karşılığıdır denilebilir. Duyu organlarımız, beynimiz, kullandığımız makineler, doğada gözlemlediğimiz bazı süreçler çeşitli girdilere göre çıktı üretirler.

Örneğin kahve makinesine kuru kahve, su ve şekeri girdi olarak verildiğinde çıktı olarak kahve verir. Cep telefonlarındaki kameralarda mercekten giren ışık bir dizi işlem sonucunda telefonun ekranındaki bir görüntüye dönüştürülür. Tıpkı bu örneklerde olduğu gibi matematikte fonksiyonlar, verilen girdi üzerine çeşitli işlemler yaparak çıktı üreten dönüştürücülerdir.

ÖRNEK: Matematikte fonksiyon kavramına model olacak bir durumu ele alalım.

Bir hastane doğumhanesinde 3 anne adayından biri ikiz, diğer ikisi ise birer çocuk dünyaya getirmiştir. Hemşireler bebekleri hazırlayıp annelerine teslim edecektir ve annesine teslim edilmeyen bebek kalmayacaktır.

Bebeklerin kümesini A kümesi, annelerin kümesini B kümesi olarak isimlendirerek aşağıdaki iki eşleştirme durumunu inceleyelim.

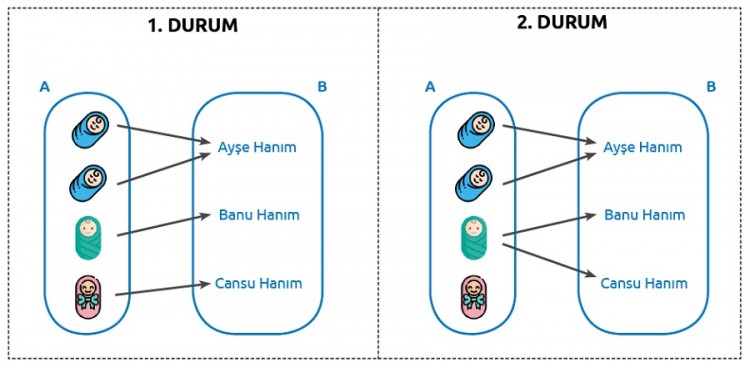
1. DURUM‘da ikizler aynı anneye teslim edilmiştir. Her bebek bir anneye teslim edilmiştir ve teslim edilmeyen bebek kalmamıştır. Bu sebeplerden dolayı bu eşleştirme uygun bir eşleştirmedir.

2. DURUM‘da bir bebeğin iki anneye teslim edilmesinin mümkün olmaması ve bebekler arasında annesine teslim edilmeyen bebek kalması sebebiyle bu eşleştirme uygun değildir.

Yukarıda verdiğimiz bu iki durumlu örnek, fonksiyon kavramı için temel oluşturacak bir modeldir. Fonksiyon kavramı, tanım kümesi ve görüntü kümesi kavramları ile tanışınca bu örneğin fonksiyonlarla ilişkisi şu şekilde olacak:

• Annesine teslim edilmeyen bebek kalmamalıdır.
  (Tanım kümesinde boşta eleman kalmamalıdır.)
• Bir bebek iki anneye teslim edilmemelidir.
  (Tanım kümesindeki her eleman değer kümesinde yalnız bir elemana eşleşmelidir.)

FONKSİYON

A ve B boş kümeden farklı iki küme olmak üzere A kümesinin her bir elemanını B kümesinin bir ve yalnız bir elemanına eşleyen ilişkiye A’dan B’ye tanımlı fonksiyon denir. Fonksiyonlar genellikle f, h, g gibi sembollerle gösterilir.

TANIM, DEĞER VE GÖRÜNTÜ KÜMESİ

A dan B ye tanımlanan f fonksiyonu f: A → B şeklinde gösterilir. A kümesine tanım kümesi, B kümesine değer kümesi denir. A kümesinin elemanlarının, f fonksiyonuyla B kümesinde eşleştiği elemanlardan oluşan kümeye görüntü kümesi denir ve f(A) ile gösterilir. Görüntü kümesi değer kümesinin alt kümesidir.

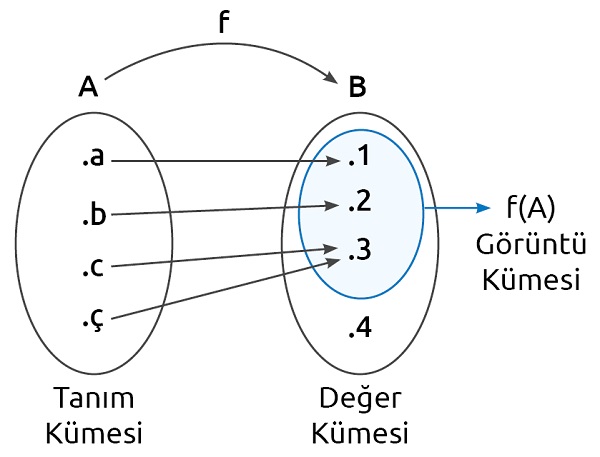
Verilen şekilde;

• f fonksiyonu A’dan B’ye tanımlı bir fonksiyondur.
• Fonksiyonun tanım kümesi A = {a, b, c, ç} dir.
• Fonksiyonun değer kümesi B = {1, 2, 3, 4} tür.
• Fonksiyonun görüntü kümesi f(A) = {1, 2, 3} tür.
• Tanım kümesinde boşta eleman kalmamıştır ve tanım kümesindeki elemanların her biri değer kümesinde yalnız bir elemanla eşleşmiştir. Bu iki şartı sağladığından f bir fonksiyondur.

BİR ELEMANIN FONKSİYON ALTINDAKİ GÖRÜNTÜSÜ

f fonksiyonu A kümesinden alınan bir x elemanını B kümesindeki bir y elemanı ile eşliyor ise x elemanının f altındaki görüntüsü y elemanıdır denir. Bu durum y = f(x) biçiminde gösterilir.

Verilen şekilde;

• a’nın f altındaki görüntüsü 1’dir. f(a) = 1
• b’nin f altındaki görüntüsü 2’dir. f(b) = 2
• c’nin f altındaki görüntüsü 3’tür. f(c) = 3
• ç’nin f altındaki görüntüsü 3’tür. f(ç) = 3

ÖRNEK: f fonksiyonu f(x) = |x + 1| şeklinde veriliyor. f(5), f(−7) ve f(0) değerlerini bulalım.

Tanım kümesindeki elemanların f altındaki görüntülerini bulmak için her bir eleman fonksiyonda x yerine yazılır.

f(x) = |x + 1|

f(5) = |5 + 1|
f(5) = 6 (5’in f altındaki görüntüsü 6’dır.)

f(−7) = |−7 + 1|
f(−7) = 6 (−7’nin f altındaki görüntüsü 6’dır.)

f(0) = |0 + 1|
f(0) = 1 (0’ın f altındaki görüntüsü 1’dir.)

FONKSİYONUN SIRALI İKİLİLERLE GÖSTERİMİ

f fonksiyonu sıralı ikililer kullanılarak da gösterilebilir. Sıralı ikililerin ilk bileşeni tanım kümesinden, ikinci bileşeni değer kümesinden yazılır.

Verilen şekilde;

f fonksiyonu f = {(a, 1), (b, 2), (c, 3), (ç, 3)} şeklinde gösterilebilir.

ÖRNEK: K’dan L’ye tanımlı bir m fonksiyonu g = {(1, 10), (2, 15), (3, 10), (4, 20)} şeklinde verilsin. Bu fonksiyonun tanım ve görüntü kümesini bulalım.

Sıralı ikililerin ilk bileşenleri tanım kümesini, ikinci bileşenleri görüntü kümesini verir.

g fonksiyonunun tanım kümesi, K = {1, 2, 3, 4}

g fonksiyonunun görüntü kümesi, g(K) = {10, 15, 20}

g fonksiyonunun değer kümesi olan L kümesini bulamayız. L kümesi görüntü kümesini kapsayan herhangi bir küme olabilir.

BİR KÜMEDE TANIMLI FONKSİYON

Tanım kümesi ve değer kümesi aynı olan, A’dan A’ya tanımlı bir fonksiyona kısaca A’da tanımlı fonksiyon denilebilir.

ÖRNEK: f: R → R, f(x) = 10x + 9 fonksiyonu verilsin.

Bu fonksiyonun hem tanım kümesi hem değer kümesi gerçek sayılar kümesi olduğu için bu fonksiyona “gerçek sayılardan gerçek sayılara tanımlı f fonksiyonu” demek yerine kısaca “gerçek sayılarda tanımlı f fonksiyonu” denilebilir.

ÇÖZÜMLÜ ÖRNEK SORULAR

ÖRNEK 1: Aşağıda verilen f fonksiyonunun tanım, değer ve görüntü kümelerini bulalım. Fonksiyonu sıralı ikililerin kümesi şeklinde yazalım.

f fonksiyonunun tanım kümesi, A = {5, 7, 6, 3}

f fonksiyonunun değer kümesi, B = {2, 8, 6, 1}

f fonksiyonunun görüntü kümesi, f(A) = {8, 6, 1}

Sıralı ikililerle f fonksiyonu, f = {(5, 8), (7, 8), (6, 1), (3, 6)}

ÖRNEK 2: Venn şemaları ile verilen aşağıdaki ifadelerden hangilerinin fonksiyon olduğunu bulalım.

f, tanım kümesindeki her bir elemanı değer kümesinde bir ve yalnız bir elemana eşlediği için fonksiyondur.

h, tanım kümesinde eşleşmeyen b elemanı kaldığı için fonksiyon değildir.

g, tanım kümesindeki a elemanı değer kümesinde birden fazla elemanla eşleştiği için fonksiyon değildir.

ÖRNEK 3: K = {a, b, c} ve L = {3, 5, 7} kümelerine göre aşağıdakilerden hangilerinin K’dan L’ye bir fonksiyon belirttiğini bulalım.

► f = {(a, 3), (a, 5), (b, 5), (c, 7)}

Tanım kümesindeki a elemanı değer kümesindeki birden fazla elemanla eşleştiği için f bir fonksiyon değildir.

► g = {(a, 5), (b, 7), (c, 7)}

Tanım kümesindeki her bir elemanı değer kümesinde bir ve yalnız bir elemana eşlediği için g bir fonksiyondur.

► h = {(a, 7), (b, 3)}

Tanım kümesinde eşleşmeyen c elemanı kaldığı için h bir fonksiyon değildir.

ÖRNEK 4: A = {−2, 0, 4} kümesi tanım kümesi olan f(x) = 3x + 5 fonksiyonunun görüntü kümesini bulalım.

Tanım kümesindeki elemanların f altındaki görüntülerini bulmak için her bir eleman fonksiyonda x yerine yazılır.

f(x) = 3x + 5

f(−2) = 3.(−2) + 5 ► f(−2) = −1

f(0) = 3.0 + 5 ► f(0) = 5

f(4) = 3.4 + 5 ► f(4) = 17

Görüntü kümesi f(A) = { −1, 5, 17 } olarak bulunur.

ÖRNEK 5: Bir f fonksiyonu f: R → R, f(x + 3) = 5x − 1 şeklinde tanımlanıyor. Buna göre f(10) değerini bulalım.

f(10)’u elde etmek için x yerine 7 yazmalıyız.

f(x + 3) = 5x − 1

f(7 + 3) = 5.7 − 1

f(10) = 34

ÖRNEK 6: Gerçek sayılarda tanımlı f(2x + 2) = 4x+1 fonksiyonu veriliyor. Buna göre f(20) değerini bulalım.

f(20)’yi elde etmek için x yerine 9 yazmalıyız.

f(2x + 2) = 4x+1

f(2.9 + 2) = 4.9+1

f(20) = 37

ÖRNEK 7: Bir f fonksiyonu f: A → B, f(x) = 2x + 1 şeklinde tanımlanıyor. Fonksiyonun görüntü kümesi f(A) = {3, 5, 7} olduğuna göre fonksiyonun tanım kümesi olan A’yı bulalım.

Görüntü kümesindeki elemanlar, tanım kümesindeki elemanların f altındaki görüntüsüdür. Bu yüzden görüntü kümesindeki her bir elemanı fonksiyona eşitleyerek bulunan x değerleri tanım kümesinin elemanlarıdır.

f(x) = 2x + 1

3 = 2x + 1 ► x = 1

5 = 2x + 1 ► x = 2

7 = 2x + 1 ► x = 3

Tanım kümesi A = { 1, 2, 3 } olarak bulunur.

matematikciler.com olarak ziyaretçilerimize ücretsiz ve nitelikli içerikler sunmak için yoğun çaba sarfediyoruz. Bu emeğin korunması adına bu konu anlatımının izinsiz yayınlanması yasaktır!