BU KONUDA ÖĞRENECEKLERİMİZ:
✓ Kesirleri Karşılaştırma
✓ Kesirleri Sıralama
Bu konumuzda öncelikle birim kesirleri sıralamayı, daha sonra bir doğal sayı ile bir bileşik kesri karşılaştırmayı göreceğiz. Son olarak payları eşit olan, paydaları eşit olan veya birinin paydası diğerinin katı olan kesirleri sıralamayı öğreneceğiz.
BİRİM KESİRLERİ SIRALAMA
Birim kesirler eş parçalara ayrılmış bir bütündeki bir parçayı temsil etmektedir. Bu sebeple paydası büyük olan birim kesirler (parça sayısı çok olacağı için) daha küçüktür.
ÖRNEK: \(\frac12\) ile \(\frac14\) kesirlerini karşılaştıralım.
\(\frac12\) kesri 2 eş parçaya ayrılmış bir bütünün bir parçasını, \(\frac14\) kesri ise 4 eş parçaya ayrılmış bir bütünün bir parçasını temsil etmektedir.
Bu yüzden bu kesirlerin sıralanışı: \(\frac14<\frac12\) olur.

BİR DOĞAL SAYI İLE BİR BİLEŞİK KESRİ KARŞILAŞTIRMA
Bir doğal sayı ile bileşik kesri karşılaştırmak için bileşik kesri tam sayılı kesre çeviririz. Kesrin tam kısmı doğal sayıya eşitse veya büyükse kesir daha büyüktür, kesrin tam kısmı doğal sayıdan küçükse kesir daha küçüktür.
ÖRNEK: 4 ile \(\frac{13}4\) kesrini karşılaştıralım.
\(\frac{13}4=3\frac14\) olduğu için tam kısmı 3’tür. Bu kesir 4 sayısından küçüktür.
ÖRNEK: 2 ile \(\frac{11}5\) kesrini karşılaştıralım.
\(\frac{11}5=2\frac15\) olduğu için tam kısmı 2’dir. Bu kesir 2 sayısından büyüktür.
PAYLARI EŞİT OLAN KESİRLERİ SIRALAMA
Payları eşit olan kesirleri sıralamak için kesirlerin paydalarına bakarız. Paydası küçük olan kesir daha büyüktür.
ÖRNEK: \(\frac26\) ile \(\frac23\) kesirlerini karşılaştıralım.
\(\frac26\) kesri 6 eş parçaya ayrılmış bir bütünün 2 parçasını,
\(\frac23\) kesri ise 3 eş parçaya ayrılmış bir bütünün 2 parçasını temsil etmektedir.
Bu yüzden bu kesirlerin sıralanışı: \(\frac26<\frac23\) olur.

PAYDALARI EŞİT OLAN KESİRLERİ SIRALAMA
Paydaları eşit olan kesirleri sıralamak için kesirlerin paylarına bakarız. Payı büyük olan kesir daha büyüktür.
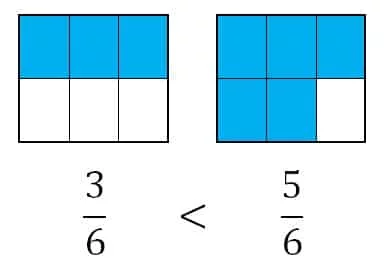
ÖRNEK: \(\frac36\) ile \(\frac56\) kesirlerini karşılaştıralım.
\(\frac36\) kesri 6 eş parçaya ayrılmış bir bütünün 3 parçasını, \(\frac56\) kesri ise 6 eş parçaya ayrılmış bir bütünün 5 parçasını temsil etmektedir.
Bu yüzden bu kesirlerin sıralanışı: \(\frac36<\frac56\) olur.
PAYDALARI EŞİT OLMAYAN KESİRLERİ SIRALAMA
Paydaları eşit olmayan kesirleri sıralamak için öncelikle kesirlerde genişletme yaparak paydalarını eşitleriz. Paydaları eşit olan kesirlerde payı büyük olan kesir daha büyüktür.
ÖRNEK: \(\frac12\) ile \(\frac34\) kesirlerini karşılaştıralım.
\(\frac12=\frac24\) olduğu için \(\frac12<\frac34\) olur.

KONUYU PEKİŞTİRMEK İÇİN:
İLGİLİ KAZANIM TESTİ BAĞLANTISI
TEST ÇÖZME BAĞLANTISI
KONU KAZANIMLARI
BU KONUYLA İLGİLİ KAZANIMLAR:
✓ Birim kesirleri sayı doğrusunda gösterir ve sıralar.
✓ Bir doğal sayı ile bir bileşik kesri karşılaştırır.
✓ Payları veya paydaları eşit kesirleri sıralar.
| ÖNCEKİ KONU | SONRAKİ KONU |
| Kesirleri Genişletme ve Sadeleştirme | Bir Çokluğun Kesir Kadarını ve Tamamını Hesaplama |
