Rasyonel Sayıların Ondalık Gösterimi ve Devirli Sayılar

BU KONUDA ÖĞRENECEKLERİMİZ:
✓ Rasyonel Sayıların Ondalık Açılımı
✓ Ondalık Sayıları Rasyonel Sayı Olarak İfade Etme
✓ Devirli Ondalık Sayılar

RASYONEL SAYILARIN ONDALIK GÖSTERİMİ

Rasyonel sayıları ondalık gösterimle de gösterebiliriz. Bunun için şu yöntemleri kullanabiliriz:

1) Paydayı 10’un Kuvveti Yapma

Paydası 10, 100, 1000 gibi 10’un pozitif tam sayı kuvveti olan veya olabilen kesirlere “ondalık sayı” denir. Ondalık sayılar aynı zamanda rasyonel sayıdır. Rasyonel sayıları ondalık gösterimle göstermek için kesri, paydası 10, 100, 1000 gibi 10’un kuvveti olacak şekilde genişletilmelidir.

ÖRNEK: \(\frac65\) rasyonel sayısını ondalık gösterimle gösterelim.

Öncelikle bu kesrin paydasını 10 yapmak için 2 ile genişletelim. Paydası 10 olduğu için 12 sayısına virgülü 1 ile 2 arasına koyarız. Çünkü 10’da bir tane sıfır vardır bu yüzden virgülden sonra bir tane rakam olmalıdır.

\(\frac65=\frac{12}{10}=1,2\) olur.

ÖRNEK: \(\frac7{20}\) rasyonel sayısını ondalık gösterimle gösterelim.

Bu kesri 5 ile genişletirsek paydası 100 olur. Payı 35, paydası 100 oldu. Paydası 100 olduğu için ve 100’de 2 tane sıfır olduğu için virgülden sonra 2 tane rakam olmalı. Virgülün önüne de sıfır koyarız.

\(\frac7{20}=\frac{35}{100}=0,35\) olur.

NOT: Paydanın 10, 100 ve 1000 yapılması için önce kesir sadeleştirilebiliyorsa sadeleştirilmelidir. Ardından uygun bir sayı ile genişletilmelidir. Aşağıda hangi sayı ile hangi sayıyı çarparsak 10’un kuvvetini bulabiliriz sorusuna bir kaç örnek verilmiştir.

100 = 4 . 25
100 = 5 . 20

1000 = 8 . 125
1000 = 20 . 50
1000 = 25 . 40

2) Payı Paydaya Bölerek Ondalık Gösterime Çevirme

Bir rasyonel sayının payını paydasına bölerek ondalık gösterimle ifade edebiliriz.

Şimdi bunu bir örnekle açıklayalım.

ÖRNEK: \(\frac35\) rasyonel sayısını ondalık gösterimle gösterelim.

3’ü 5’e bölerken 3’ün içinde 5 olmadığı için 3’ün yanına bir tane sıfır koyarız ve bölüm kısmına virgül koyarız. Daha sonra 30’u 5’e böler 6 buluruz.

ÖRNEK: \(-\frac14\) rasyonel sayısını ondalık gösterimle gösterelim.

1’in içinde 4 olmadığı için 1’in yanına sıfır ekleriz, bölüme virgül koyar ve böleriz. Daha sonra 2’nin yanına bir tane sıfır ekleriz. Burada eklediğimiz sıfır için bölümde bir değişiklik yapmayız. Sonuç −0,25 olur.

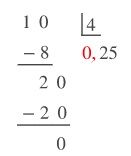
ÖRNEK: \(\frac79\) sayısını ondalık gösterimle gösterelim.

Bu örnekte görüldüğü gibi bazı sayıların ondalık gösterimlerinde sonsuza kadar tekrar eden sayılar bulunur. Aşağıda bunları devirli ondalık sayılar olarak anlatacağız.

ONDALIK GÖSTERİMLERİ RASYONEL SAYI OLARAK YAZMA

Ondalık sayı virgül yokmuş gibi paya yazılır. Paydadaki 1’in yanına ise sayıda virgülden sonra kaç tane rakam varsa o kadar 0 konulur.

ÖRNEK: 1,2 sayısını rasyonel sayı olarak ifade edelim.

Paya 12 yazarız. Sayıda virgülden sonra 1 tane rakam olduğu için paydaya 10 yazılır.

\(1,2=\frac{12}{10}\) olur.

ÖRNEK: 3,14 sayısını rasyonel sayı olarak yazalım.

Paya 314 yazarız ve paydaya 100 yazarız. En son sadeleştirme yaparız.

\(3,14=\frac{314}{100}=\frac{157}{50}\) olur.

DEVİRLİ ONDALIKLI SAYILAR

Bir rasyonel sayı ondalık gösterimi ile yazıldığında, ondalık kısmındaki sayılar belirli bir rakamdan sonra sonsuza kadar tekrar ediyorsa bu tür ondalık gösterimlere devirli ondalık gösterim denir. Devirli ondalık sayılarda tekrar eden rakamların üzerine devir çizgisi konularak gösterilir.

ÖRNEK: \(\frac23\) sayısını ondalık gösterimle yazalım.

Bu sayıyı ondalık gösterimle gösterirsek şunu buluruz: \(\frac23=0,6666…=0,\overline6\)

Burada 6 sayısı tekrar ettiği için 6’nın üzerine çizgi koyarız. Bu çizgi 6’nın tekrar ettiği anlamına gelir.

ÖRNEK: \(\frac{25}{11}\) rasyonel sayısının ondalık gösterimini hesap makinesiyle bulalım.

Hesap makinesinde 25’i 11’e bölersek şu sonuca ulaşırız: \(\frac{25}{11}=2,272727272…=2,\overline{27}\)

Devirli Ondalık Sayıları Rasyonel Sayıya Dönüştürme

Devirli ondalık sayıları rasyonel sayıya dönüştürürken (kesir haline) şu adımlar takip edilir:

1) Virgül ve devir çizgisi dikkate alınmadan okunan sayıdan, üzerinde devir çizgisi olmayan sayı çıkarılır ve paya yazılır.

2) Paydaya ise virgülden sonraki devreden basamak sayısı kadar 9 yazılır ve yanına devretmeyen sayı kadar sıfır yazılır.

FORMÜL: \(\frac{\overbrace{Sayının\;Tamamı\;-\;Devretmeyen\;Kısım}^{virgüle\;bakılmaksızın}}{\underbrace{\;Devreden\;rakam\;kadar\;9\;\;Devretmeyen\;rakam\;kadar\;0}_{virgülden\;sonrası\;için}}\)

FORMÜLE ÖRNEK: a,b,c,d,e birer rakam olmak üzere:

ÖRNEK: 1,234343434… sayısını kesir olarak yazacak olursak (devreden sayı 34 olduğu için 34’ün üzerinde devir çizgisi olur); \(1,234343434…\;=\;1,2\overline{34}\) sayısında yukarıdaki kuralı uygularız.

\(\frac{1234-12}{990}=\frac{1222}{990}\) bulunur.

KONUYU PEKİŞTİRMEK İÇİN: