Rasyonel Sayılar ve Sayı Doğrusunda Gösterme

BU KONUDA ÖĞRENECEKLERİMİZ:
✓ Rasyonel Sayı Nedir?
✓ Rasyonel Sayı mı? Değil mi?
✓ Rasyonel Sayıları Sayı Doğrusunda Gösterme

RASYONEL SAYILAR

a bir tam sayı ve b sıfırdan farklı bir tam sayı olmak üzere \(\frac ab\) şeklinde yazılabilen sayılara rasyonel sayılar denir. Sıfırdan büyük rasyonel sayılara pozitif rasyonel sayılar denir, sıfırdan küçük rasyonel sayılara negatif rasyonel sayılar denir.

ÖRNEK: Aşağıda bazı sayıların rasyonel sayı oldukları \(\frac ab\) şeklinde yazılarak gösterilmiştir.

► \(\frac{-2}3\)

► \(1\frac35 = \frac85\)

► \(2,8 = \frac{28}{10}\)

Her doğal sayı ve tam sayı aynı zamanda paydası 1 olan rasyonel sayıdır.

ÖRNEK: Aşağıda bazı sayıların rasyonel sayı oldukları \(\frac ab\) şeklinde yazılarak gösterilmiştir.

► \(15 = \frac{15}{1}\)

► \(-9 = \frac{-9}{1}\)

► \(0 = \frac{0}{1}\)

Görüldüğü gibi bu zamana kadar gördüğümüz doğal sayılar, tam sayılar, ondalık sayılar, devirli sayılar aynı zamanda rasyonel sayıdır. Ancak rasyonel olmayan sayılar (pi sayısı gibi) da mevcuttur ve bunlar ileriki yıllarda öğrenilecektir.

Rasyonel sayı tanımında yer alan \(\frac ab\) ifadesinde paydada yer alan “b” sayısının sıfırdan farklı olması şarttır. “a” sayısı için ise böyle bir şart yoktur. Eğer payda sıfır olursa ortaya çıkan ifade rasyonel sayı olmaz.

Sıfırın, sıfır hariç bir sayıya bölümü sıfırdır.

ÖRNEK: \(\frac02\;,\;\frac0{-3}\) sayıları 0’a eşittir ve rasyonel sayıdır.

Sıfır hariç bir sayının sıfıra bölümü tanımsızdır.

ÖRNEK: \(\frac70\;,\;\frac{-1}0\) ifadeleri tanımsızdır ve bu ifadeler rasyonel sayı değildir.

Sıfırın sıfıra bölümü belirsizdir.

ÖRNEK: \(\frac00\) belirsizdir ve bu ifade rasyonel sayı değildir.

Bir rasyonel sayıda “−” işaretinin payda, paydada ya da kesir çizgisinin önünde olması rasyonel sayının değerini değiştirmez.

ÖRNEK: \(\frac{-2}3=\frac2{-3}=-\frac23\) gibi.

RASYONEL SAYILARI SAYI DOĞRUSUNDA GÖSTERME

Rasyonel sayılar sayı doğrusunda gösterilirken önce tam sayılı kesre dönüştürülür. Sonra tam kısmı kadar ilerlenir. (Pozitifse sağa, negatifse sola doğru) Daha sonra bu tam sayı ile bir sonraki tam sayı ile arası kesrin paydası kadar parçaya bölünür ve kesrin payı kadar ilerlenir. Bu ilerleme negatif sayılarda sola doğru pozitif sayılarda sağa doğrudur. Yani 0’dan uzaklaşırız.

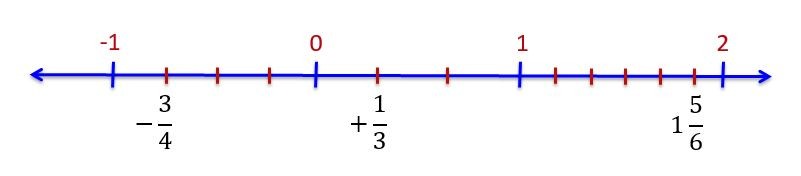
Yukarıdaki örneğe bakacak olursak \(1\frac56\) kesri 1 ile 2 arasındadır. Dolayısıyla 1 ile 2 arası 6 parçaya bölünür ve 5 parça ilerlenip sayının yeri bulunur.

\(-\frac34\) kesrine bakacak olursak bu basit kesir olduğu için 0 ile −1 arasındadır ve bu aralık 4 parçaya bölünür. Bu parçalardan sola doğru 3 parça ilerlenir ve kesrin yeri bulunmuş olur.

ÖRNEK: Aşağıdaki sayı doğrularında soru işareti yerine gelmesi gereken sayıları bulalım.

İlk sayı doğrusunda sayı −1 ile −2 arasında olduğu için sayının tam kısmı −1’dir. −1 ile −2 arasını 5 parçaya bölmüş ve bize sorulan parça üçüncü. (0’ın olduğu taraftan sayıyoruz.)

Buna göre sayımız \(-1\frac35\)

İkinci sayı doğrusunda sayımız 0 ile −1 arasında olduğu için basit kesirdir. 3 parçaya bölünmüş ve 1. parça olduğu için soru işareti yerine \(-\frac13\) gelmelidir.

Üçüncü sayı doğrusunda sayımız 0 ile 1 arasında olduğu için basit kesirdir ve 4 parçadan 3.sü olduğu için \(\frac34\)‘tür.

KONUYU PEKİŞTİRMEK İÇİN: