Kareköklü Sayılara Giriş ve Tam Kare Sayılar

BU KONUDA ÖĞRENECEKLERİMİZ:
√ Kareköklü İfadeler
√ Tam Kare Sayılar
√ Tam Kare Sayıların Karekökünü Bulma

KAREKÖK NEDİR?

Verilen sayının hangi sayının karesi olduğunu bulma işlemine karekök alma işlemi denir.Karekök ” \(\sqrt\;\) ” sembolü ile gösterilir. \(\sqrt x\) sayısı “karekök x” şeklinde okunur.

Negatif bir sayının karekökü alınamaz çünkü negatif bir sayı hiç bir sayının karesi olamaz.

Şimdi karekökü daha iyi kavramak için bir örnek verelim.

ÖRNEK: 9 hangi sayının/sayıların karesidir bulalım.

9 = 3.3 = 3²

9 = (-3).(-3) = (-3)² olduğundan

9 hem 3’ün hem de -3’ün karesidir.

\(\sqrt\;\) sembolü, bir sayının pozitif karekökünü bulmak için kullanılır.

ÖRNEK: \(\sqrt9\) sayısının değerini bulalım.

Bir önceki örnekte gördüğümüz gibi 9, 3 ve -3’ün karesidir. Karekök işlemi de bir sayının hangi sayının karesi olduğunu bulmadır.

Bu yüzden \(\sqrt9\) = 3’tür.

TAM KARE SAYILAR VE KAREKÖKLERİ

Bir tam sayının karesi olan, diğer bir ifade ile karekökü tam sayı olan doğal sayılara tam kare sayılar denir. Tam kare sayılara karesel sayılar da denir.1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 192, 256, 289, … sayıları tam kare sayılardır.

Tam kare sayıların karekökleri tam sayıdır.

Aşağıdaki şekilde de görüldüğü gibi 1, 4, 9 gibi tam kare sayılarla kenarları tam sayı olan kareler elde edilebiliyor. Ancak 2, 3, 5, 7 gibi sayılarla kenarları tam sayı olan kareler elde edilemiyor.

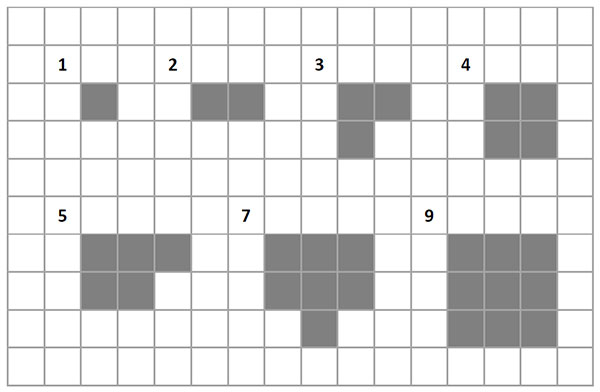
Kenar uzunluğu verilen bir karenin alanını bulmak için kenar uzunluğunun karesi alındığı gibi, alanı verilen bir karenin bir kenarının uzunluğunu bulmak için alanının karekökünü alırız.

ÖRNEK: Alanı 25 br² olan bir karenin bir kenarı kaç birimdir?

Kenarı = \(\sqrt{25}\) = 5 birimdir.

ÖRNEK: 18 adet birim karoya en az kaç tane daha eklenirse bir kare oluşur?

18’den büyük en küçük tam kare sayı 25 olduğu için:

25 – 18 = 7 tane daha birim karo eklenmelidir.

Bir sayının hangi sayının karesi olduğunu bulmak için çarpanlarına ayırabiliriz.

ÖRNEK: \(\sqrt{196}\) sayısının değerini bulalım.