Kenarortay, Açıortay ve Yükseklik

BU KONUDA ÖĞRENECEKLERİMİZ:
✓ Üçgende Yardımcı Elemanlar
✓ Kenarortay, Açıortay, Yükseklik
✓ Özel Durumlar, Muhteşem Üçlü

KENARORTAY

Bir üçgenin herhangi bir kenarının orta noktasını, karşı köşe noktası ile birleştiren doğru parçasına üçgenin o kenarına ait kenarortayı denir. “a” kenarına ait kenarortay V_a sembolü ile gösterilir.

Yukarıdaki resimde [AB] kenarına ait kenarortay [CD], [BC] kenarına ait kenarortay [AF], [CA] kenarına ait kenarortay [BE]’dır.

Kenarortaylar üçgenin iç bölgesindeki bir noktada (G noktasında) kesişmiştir.

Tüm üçgenlerde kenarortayların kesişim noktası üçgenin iç bölgesindedir. Bu noktaya Ağırlık Merkezi denir ve G harfiyle gösterilir.

YÜKSEKLİK

Bir üçgenin bir köşesinden karşı kenarına indirilen dik doğru parçasına üçgenin o kenarına ait yüksekliği denir. “a” kenarına ait yükseklik h_a sembolü ile gösterilir.

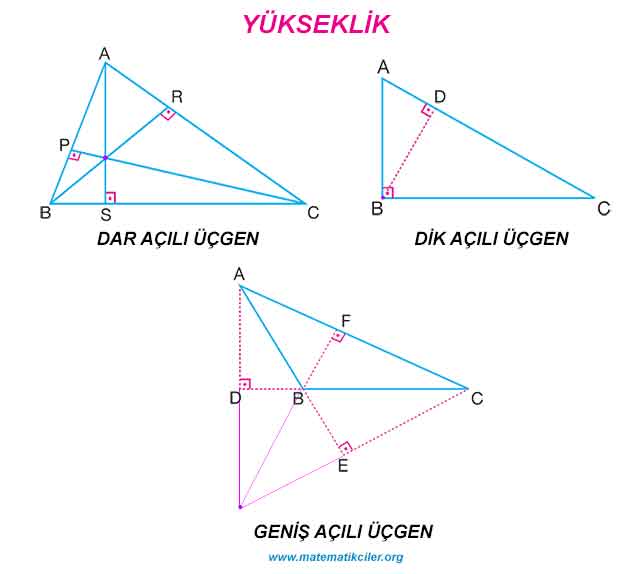
Resimdeki dar açılı üçgende: [AB] kenarına ait yükseklik [CP], [BC] kenarına ait yükseklik [AS], [CA] kenarına ait yükseklik [BR]’dır.

Resimdeki dik açılı üçgende: [AB] kenarına ait yükseklik [BC], [BC] kenarına ait yükseklik [AB], [CA] kenarına ait yükseklik [BD]’dır.

Resimdeki geniş açılı üçgende: [AB] kenarına ait yükseklik [CE], [BC] kenarına ait yükseklik [AD], [CA] kenarına ait yükseklik [BF]’dır.

Yüksekliklerin kesişim noktası mor renkli noktadır. Yükseklikler dar açılı üçgende üçgenin iç bölgesinde, dik açılı üçgende üçgenin köşesinde, geniş açılı üçgende üçgenin dış bölgesinde kesişmiştir.

Yüksekliklerin kesişim noktası dar açılı üçgenlerde üçgenin iç bölgesinde, dik açılı üçgenlerde üçgenin üzerinde (dik köşesinde), geniş açılı üçgenlerde ise üçgenin dış bölgesindedir. Bu noktaya Diklik Merkezi adı verilir.

AÇIORTAY

Bir üçgenin herhangi bir iç açısını iki eş parçaya ayırarak köşeyi karşı kenara birleştiren doğru parçasına üçgenin iç açıortayı denir. “A” açısına ait açıortay n_A sembolü ile gösterilir.

Yukarıdaki resimde [AB] kenarına ait açıortay [CP], [BC] kenarına ait açıortay [AS], [CA] kenarına ait açıortay [BR]’dır.

Tüm üçgenlerde açıortayların kesişim noktası üçgenin iç bölgesindedir.

NOT: Çeşitkenar üçgende bir kenara ait yükseklik, açıortay ve kenarortay arasında; yükseklik < açıortay < kenarortay bağıntısı vardır.

NOT: Eşkenar üçgende bir açının açıortayı ile o açının karşısındaki kenarın kenarortayı ve yüksekliği aynı doğru parçasıdır. Aynı eşitlik ikizkenar üçgendeki eş kenarlar arasında kalan açının açıortayı ile karşı kenarının kenarortay ve yüksekliğinde de vardır.

KENAR ORTA DİKME

Kenar orta dikme 8. sınıf müfredatından kaldırıldı ancak soru bankalarında karşınıza çıkan bir terim olduğu için aşağıdan kenar orta dikme nedir öğrenebilirsiniz.

Üçgenin herhangi bir kenarının orta noktasından geçen ve bu kenara dik olan doğru parçasına kenar orta dikme denir.

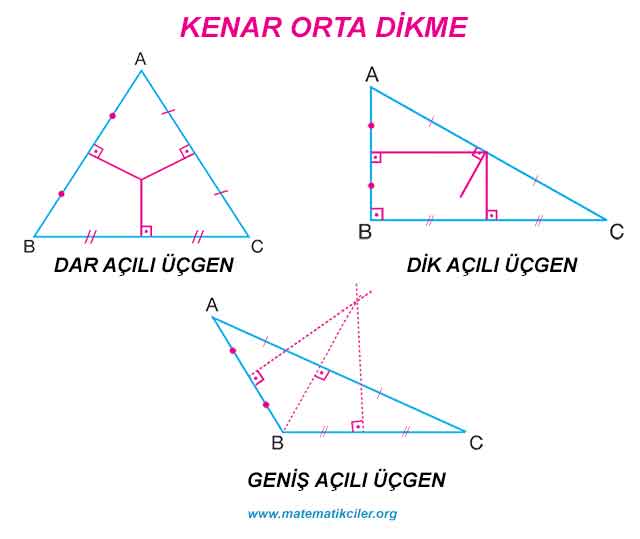
Kenar orta dikmeler dar açılı üçgenlerde üçgenin iç bölgesinde, dik açılı üçgenlerde üçgenin üzerinde (hipotenüsün orta noktasında) , geniş açılı üçgenlerde ise üçgenin dış bölgesinde bir noktada kesişir.

KONUYU PEKİŞTİRMEK İÇİN: