Üçgen Eşitsizliği ve Açı Kenar Bağıntıları

BU KONUDA ÖĞRENECEKLERİMİZ:
✓ Üçgenlerin Kenar Uzunlukları Arasındaki İlişki
✓ Üçgenlerin Kenar Uzunlukları ile Açılarının Ölçüleri Arasındaki İlişkileri

ÜÇGENLER

Doğrusal olmayan üç noktayı birleştiren doğru parçalarının meydana getirdiği şekle üçgen denir.

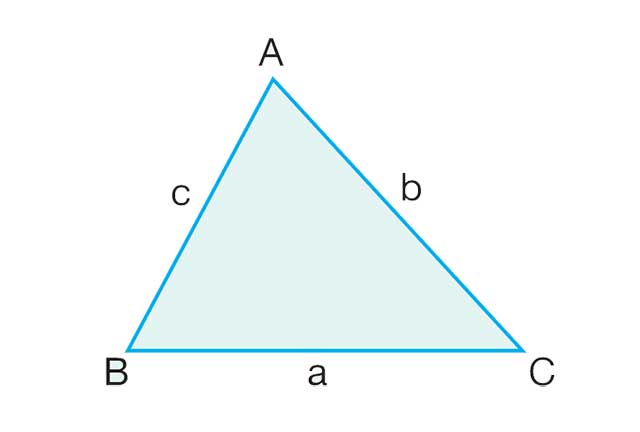
KÖŞELERİ: A, B ve C noktaları üçgenin köşeleridir.

KENARLARI: [AB], [BC] ve [AC] üçgenin kenarlarıdır.

KENAR UZUNLUKLARI: a, b ve c üçgenin kenar uzunluklarıdır.

ÜÇGENLERİN KENAR UZUNLUKLARI ARASINDAKİ İLİŞKİ

Bir üçgende bir kenarın uzunluğu diğer iki kenarın uzunlukları toplamından küçük, farkının mutlak değerinden büyüktür. Bu eşitsizliğe üçgen eşitsizliği denir.

Yukarıdaki ABC üçgeni için:

a + b > c > |a−b|

a + c > b > |a−c|

b + c > a > |b−c| olur.

ÖRNEK: Aşağıdaki mavi, kırmızı ve siyah çubukları uç uca ekleyerek üçgen oluşturulabilir mi?

Üç tane doğru parçasını uç uca ekleyerek üçgen elde etmek istiyorsak bu doğru parçalarından herhangi birinin uzunluğu, diğer ikisinin uzunluğunun toplamından kısa, farkından uzun olmalıdır.

Yukarıdaki örnekleri inceleyelim.

1. ŞEKİL:

3cm, 4cm, 5cm uzunluğunda üç tane çubuğu uç uca ekleyerek üçgen oluşturabiliriz.

Çünkü bir kenar uzunluğu diğerlerinin toplamından küçük, farkından büyüktür.

4+3 > 5 > 4−3

7 > 5 > 1

2. ŞEKİL:

1cm, 3cm, 5cm uzunluğundaki üç tane çubuğu uç uca ekleyerek üçgen oluşturamayız.

Çünkü bir kenar diğer ikisinin toplamından uzundur.

3+1 > 5 > 3−1

4 > 5 > 2 (4 sayısı 5’ten büyük değildir.)

ÖRNEK: Aşağıda verilen uzunluklara göre belirtilen üçgenlerin çizilip çizilemeyeceğini bulalım.

1) |AB| = 8 cm , |AC| = 4 cm , |BC| = 10 cm olan bir ABC üçgeni:

İki kenarı toplar, diğer kenardan büyük mü diye bakarız.

8+4   = 12 > 10

8+10 = 18 > 4

4+10 = 14 >8

olduğu için çizilebilir.

2) |DE| = 3 m , |EF| = 5,5 m , |DF| = 9 m olan bir DEF üçgeni:

3 + 5,5   = 8,5 > 9   (8,5 sayısı 9’dan büyük değildir.)

5,5 + 9  = 14,5 > 3

3 + 9     = 12 > 5,5

olduğu için çizilemez.

ÖRNEK: Bir üçgenin iki kenarının uzunlukları 15 cm, 12 cm ise diğer kenarının uzunluğu kaç cm olabilir?

Verilmeyen kenarın uzunluğuna x dersek bu kenarın uzunluğuna dair üçgen eşitsizliğini yazarız.

15 + 12 > x > 15 − 12

27 > x > 3

Bu kenarın uzunluğu 27 cm ile 3 cm arasında olabilir.

ÖRNEK:

ÜÇGENDE AÇI KENAR BAĞINTILARI

► Bir üçgende küçük açı karşısında kısa kenar, büyük açı karşısında uzun kenar vardır.

\(s\left(\widehat A\right)>s\left(\widehat B\right)>s\left(\widehat C\right)\) ise a > b > c olur.

► Eğer açılar eşit ise bu açıların karşısındaki kenarlar da eşittir.

# Dik açılı üçgenlerde, dik açıdan daha büyük açı olamayacağı için hipotenüsün (dik açının karşısındaki kenar) uzunluğu dik kenarların uzunluklarından daha büyüktür.

# Geniş açılı üçgenlerde geniş açıdan daha büyük açı olamayacağı için en uzun kenar geniş açının karşısındakidir.

ÖRNEK: Aşağıda iki iç açısının ölçüsü verilen üçgenlerin kenar uzunluklarını büyükten küçüğe doğru sıralayalım.

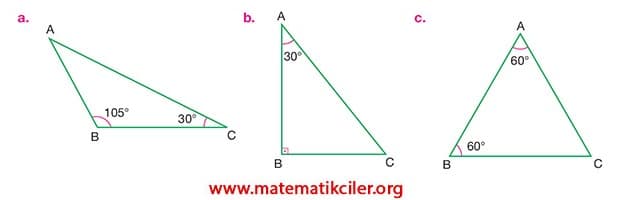
Sorunun a şıkkındaki üçgende:

Verilmeyen A açısının ölçüsünü buluruz.

105° + 30° = 135°

180° − 135° = 45°

Şimdi açıların büyüklüğüne göre kenarları sıralarız: |AC| > |BC| > |AB|

Sorunun b şıkkındaki üçgende: 

Verilmeyen B açısının ölçüsünü buluruz.

90° + 30° = 120°

180° − 120° = 60°

Şimdi açıların büyüklüğüne göre kenarları sıralarız: |AC| > |AB| > |BC|

Sorunun c şıkkındaki üçgende: 

Verilmeyen C açısının ölçüsünü buluruz.

60° + 60° = 120°

180° − 120° = 60°

Eşit açıların karşısındaki kenarların uzunlukları eşit olduğu için: |AC| = |AB| = |BC|

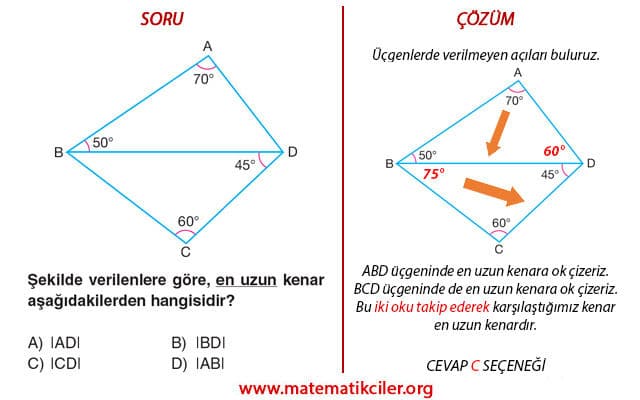
ÖRNEK:

KONUYU PEKİŞTİRMEK İÇİN: