- BU KONUDA ÖĞRENECEKLERİMİZ:
- √ Trigonometri ile ilgili problemler nasıl çözülür?
Dik üçgendeki dar açıların trigonometrik oranlarını öğrendik. Hatta 30, 45 ve 60 derecelik açıların trigonometrik oranlarının değerlerini biliyoruz. Şimdi bu bilgilerimizi problem çözmede kullanmaya geldi sıra. Trigonometri ile ilgili problemlere geçmeden önce Trigonometri konu anlatımına göz atmanızda fayda var: Trigonometri
PROBLEM-1
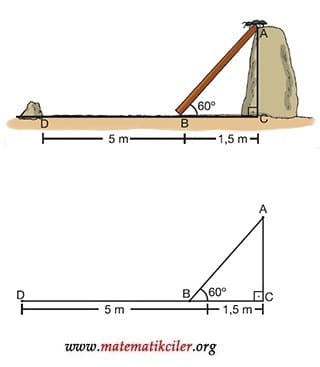Bir kayaya dayalı duran dal parçasının üst ucunda bulunan karınca, bulduğu buğday tanesini yuvasına götürmek istiyor. Buna göre buğday tanesini yuvasına kadar kaç metre taşımalıdır?
ÇÖZÜM: Şekilde oluşan üçgeni çizersek 30° – 60° – 90° üçgeni oluşur. ABC üçgeninde 30°’nin karşısındaki kenarın uzunluğu 1,5 metredir. Sin30° = 0,5 olduğu için hipotenüsün uzunluğu 30°’nin karşısındaki kenarın uzunluğunun 2 katıdır. Bu yüzden dal parçasının uzunluğunu 3 metre buluruz.
Yuvasına varmak için dal uzunluğu ile 5 metreyi toplamalıyız.
5 + 3 = 8 metre cevabını buluruz.
PROBLEM-2
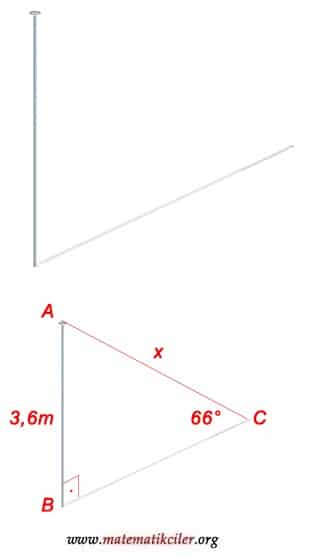3,6 metre boyundaki bir direğin gölgesi ile Güneş ışınlarının yaptığı açı 66°’dir. Verilenlere göre gölgenin bitim noktasının direğin tepesine olan uzaklığı kaç metredir? (sin 66° ∼ 0,9)
ÇÖZÜM: Soruda verilenleri geometrik olarak çizersek bir dik üçgen oluşur. Bu dik üçgende 66 derecelik bir açı, bu açının karşısındaki kenarın uzunluğu verilmiştir ve hipotenüsün uzunluğu sorulmaktadır.
Bu üçgende 66 derecelik açının sinüsünü yazacak olursak: \(\sin\;66^\circ\;=\;\frac{3,6}x\)
Sorunun sonunda 66 derecenin sinüsünün yaklaşık olarak 0,9 olduğu verilmiştir. O zaman az önce yazdığımız oranı bu sayıya eşitler ve bir orantı oluştururuz.
\(\frac{3,6}x=\frac9{10}\)Son olarak içler-dışlar çarpımı yaparak sonucu buluruz.
9 . x = 10 . 3,6
9x = 36
x = 4 metre
PROBLEM-3
Bir arazi aracı zeminle 30°’lik açı yapan bir yolda 100 m ilerliyor ve daha sonraki \(80\sqrt2\) m’lik yolda yolun zeminle yaptığı açı 15° daha artıyor. Araç A noktasına ulaştığında yerden yüksekliği kaç metre olur?
ÇÖZÜM: Şekli geometrik olarak çizersek iki tane dik üçgen oluşur. Bunlardan biri 30-60-90 üçgeni, diğeri ise 45-45-90 üçgeni. Bu üçgenlerdeki dar açıların trigonometrik oranlarını biliyoruz. Bu bilgilerimize dayanarak soruyu şu şekilde çözeriz:
CDE üçgeninde hipotenüsün uzunluğu 100 m olduğu için 30°’un karşısındaki kenarın yani CD kenarının uzunluğu hipotenüsün yarısıdır. (50 metre)
ABC üçgeninde hipotenüsün uzunluğu \(80\sqrt2\) olduğu için 45°’nin karşısındaki kenarın yani AB kenarının uzunluğu hipotenüsün \(\sqrt2\)‘ye bölümüdür. (80 metre)
Araç A noktasına geldiğinde yerden yüksekliği: 50 + 80 = 130 metre olur.