BU KONUDA ÖĞRENECEKLERİMİZ:
✓ Yamuğun alanı nasıl bulunur?
✓ Yamuğun alan formülü
✓ Dik yamuğun alanı
YAMUĞUN ALANI
Yamuğun alanı, taban kenarlarının uzunlukları toplamı ile yükseklik uzunluğunun çarpımının yarısına eşittir.
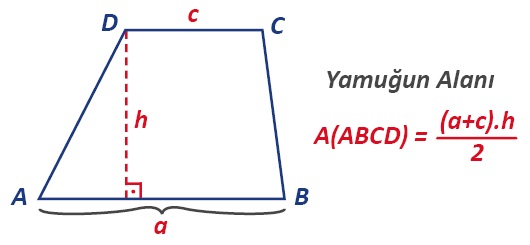
Yamuğun Alan Formülü İspatı
Yamuğun bir köşegeni çizilirse iki tane üçgen oluşur. Bu iki üçgenin alanları ayrı ayrı bulunup toplanarak da yamuğun alanı hesaplanabilir.
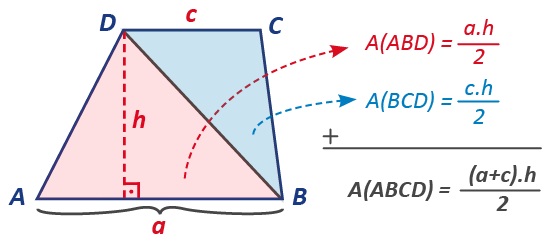
Örneğin yukarıdaki yamukta [DB] köşegeni çizilince tabanı a olan ve yüksekliği h olan bir üçgen ve tabanı c olan ve yüksekliği h olan ikinci bir üçgen elde edilir.
İlk üçgenin alanı \(\frac{a.h}{2}\), ikinci üçgenin alanı \(\frac{c.h}{2}\) olur.
Bu alanları toplarsak \(\frac{a.h}{2} + \frac{c.h}{2} = \frac{a.h + c.h}{2} = \frac{(a+c).h}{2}\) elde ederiz.
ÖRNEK: Aşağıda taban kenar uzunlukları ve yüksekliği verilen yamuğun alanını bulalım.
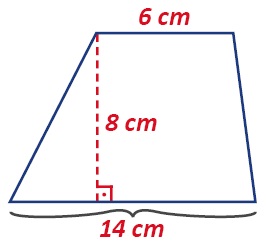
Yamuğun alanını bulmak için alt taban uzunluğu ile üst taban uzunluğunu toplar, yükseklikle çarpar ve 2’ye böleriz.
\(\frac{(6+14).8}{2}\) = \(\frac{20.8}{2}\) = 80 cm2
ÖRNEK: Aşağıda noktalı kağıt üzerinde verilen yamuğun alanını bulalım.

Verilen yamuğun;
alt tabanı 6 birim,
üst tabanı 3 birim,
yüksekliği 3 birimdir.
Yamuğun alanını formülle şu şekilde buluruz:
\(\frac{(6+3).3}{2}\) = \(\frac{9.3}{2}\) = 13,5 br2
ÖRNEK: Aşağıda taban kenar uzunlukları ve yüksekliği verilen yamuğun alanını bulalım.
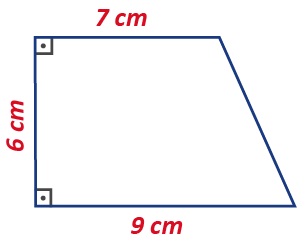
Dik yamuğun tabanlara dik olan kenarı aynı zamanda yamuğun yüksekliğidir.
\(\frac{(7+9).6}{2}\) = \(\frac{16.6}{2}\) = 48 cm2
KONUYU PEKİŞTİRMEK İÇİN:
İLGİLİ KAZANIM TESTİ BAĞLANTISI
KONU KAZANIMLARI
BU KONUYLA İLGİLİ KAZANIMLAR:
✓ Eşkenar dörtgen ve yamuğun alan bağıntılarını oluşturur, ilgili problemleri çözer.
| ÖNCEKİ KONU | SONRAKİ KONU |
| Eşkenar Dörtgenin Alanı | Dikdörtgende Çevre Alan İlişkisi |
