Çarpanlar ve Asal Çarpanlar

BU KONUDA ÖĞRENECEKLERİMİZ:
✓ Pozitif Tam Sayıların Pozitif Çarpanlarını Bulma
✓ Pozitif Tam Sayıların Asal Çarpanlarını Bulma
✓ Pozitif Tam Sayıları Üslü İfade veya Üslü İfadelerin Çarpımı Şeklinde Yazma

Bir doğal sayının çarpanlarını bulmayı 6. sınıfta çarpanlar ve katlar konusunda öğrenmiştik. Asal sayılar ve bir doğal sayının asal çarpanlarını bulmayı da yine 6. sınıfta asal sayılar ve asal çarpanlar konusunda öğrenmiştik. 8. sınıf çarpanlar ve katlar konusunun ilk kazanımı olan bu konuda ise bunları hatırlayıp, pozitif tam sayıları üslü ifade veya üslü ifadelerin çarpımı şeklinde yazmayı öğreneceğiz.

BİR DOĞAL SAYININ ÇARPANLARI (BÖLENLERİ)

Her doğal sayı iki doğal sayının çarpımı olarak yazılabilir. Bu iki sayıdan her birine o sayının çarpanı denir. Bu çarpanlar aynı zamanda o sayıyı kalansız böldüğü için bir doğal sayının çarpanları aynı zamanda bölenleridir.

Çarpanları yazarken 1’den başlayarak son yazdığımız çarpanlara eşit olana kadar sırayla gitmek işlemlerinizi kolaylaştırır. Ayrıca bölünebilme kuralları konusunu tekrar ederseniz bu konuda ve sonraki konularda faydasını görürsünüz.

ÖRNEK: 24 sayısının pozitif çarpanlarını (kalansız bölenlerini) bulalım.

24’ü iki sayının çarpımı şeklinde yazalım. Aşağıdaki gibi sonuçlar elde ederiz.

24 = 1 x 24
24 = 2 x 12
24 = 3 x 8
24 = 4 x 6
24 = 6 x 4 Bir üstte aynısını yazmıştık, bu yüzden işlemimiz bitti.

Buna göre yukarıda yazdığımız sayılar 24’ün çarpanlarıdır. Bu çarpanlar aynı zamanda 24’ün kalansız bölenleridir.

24’ün Pozitif Çarpanları / Bölenleri = 1, 2, 3, 4, 6, 8, 12, 24

ÖRNEK: 60 sayısının pozitif çarpanlarını bulalım.

60’ı iki sayının çarpımı şeklinde yazarsak aşağıdaki sonuçları elde ederiz.

60 = 1 x 60
60 = 2 x 30
60 = 3 x 20
60 = 4 x 15
60 = 5 x 12
60 = 6 x 10

60’ın Pozitif Çarpanları (Bölenleri) = 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 ve 60’tır.

ASAL SAYILAR

Pozitif çarpanları (bölenleri) sadece 1 ve kendisi olan 1’den büyük sayılara asal sayılar denir.

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, … sayıları birer asal sayıdır.

ÖRNEK: 91 asal sayı mıdır? 91’in çarpanlarını bulalım.

91 = 1 x 91

91 = 7 x 13

Görüldüğü gibi 91 sayısının çarpanları arasında 1 ve kendisinden başka sayılar da vardır. Bu yüzden 91 sayısı asal sayı değildir.

► 1 asal sayı değildir, en küçük asal sayı 2’dir

► 2’den başka çift asal sayı yoktur. (Çünkü hepsi 2’ye de bölünür.)

► 1’den 200’e kadar olan asal sayılar için tıklayınız.

ASAL ÇARPANLAR

Bir sayının çarpanlarından asal olanlarına bu sayının asal çarpanları denir.

ÖRNEK: 75 sayısının asal çarpanlarını bulalım.

75 sayısının tüm çarpanlarını yukarıda öğrendiğimiz yöntemle 1, 3, 5, 15, 25, 75 olarak buluruz.

Bu çarpanlar arasında asal sayı olanlar 3 ve 5 olduğu için 75’in asal çarpanları 3 ve 5’tir.

► Sayıların asal çarpanlarını bulmayı ve bir sayıyı asal çarpanlarının çarpımı şeklinde yazmayı aşağıdaki iki yöntemle yapabiliriz.

1) Çarpan Ağacı

Çarpan ağacı nedir, nasıl yapılır görelim.

Bir sayıyı iki sayının çarpımı şeklinde yazarız (en küçük asal sayıdan başlayabiliriz). Daha sonra bulduğumuz sayıları asal sayı olana kadar bu işleme devam ederiz. Oluşan dalların uçlarındaki sayılar sayımızın asal çarpanlarıdır

Çarpan ağacında dalların uçlarındaki asal sayıların çarpımı, çarpanlarına ayırdığımız sayıyı verir. Bir sayıyı bu şekilde yazarsak asal çarpanlarının tabanlarda bulunduğu üslü ifadelerin çarpımı şeklinde yazmış oluruz.

ÖRNEK: 36 sayısını çarpan ağacı kullanarak asal çarpanlarına ayıralım.

36 sayısının çarpanları : 1, 2, 3, 4, 6, 9, 12, 18, 36’dır. Bunu bir sayının çarpanları konumuzda öğrenmiştik. Bu sayılardan asal sayı olanları asal çarpanlarımızdır.

36 sayısının asal çarpanları: 2 ve 3’tür. Şimdi bunu çarpan ağacı ile bulalım:

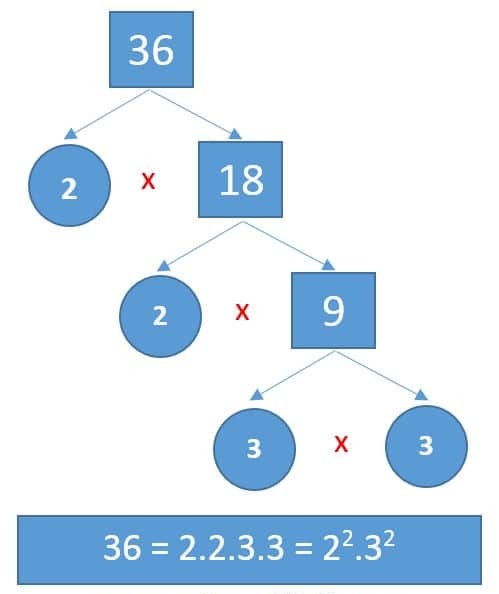
36 sayısının asal çarpanlarının çarpımı şeklinde yazılmış hali 36 = 2² . 3² ‘dir.

ÖRNEK: 60 sayısını çarpan ağacı kullanarak asal çarpanlarına ayıralım.

60 sayısının çarpanları : 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 ve 60’tır.

60 sayısının asal çarpanları: 2, 3 ve 5’tir. Şimdi bunu çarpan ağacı ile bulalım:

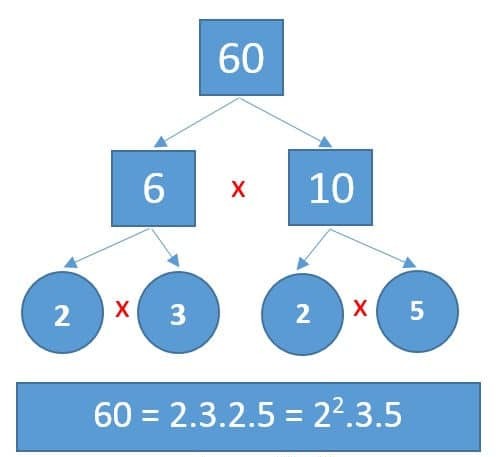
60 sayısının asal çarpanlarının çarpımı şeklinde yazılmış hali 60 = 2² . 3 . 5 ‘tir.

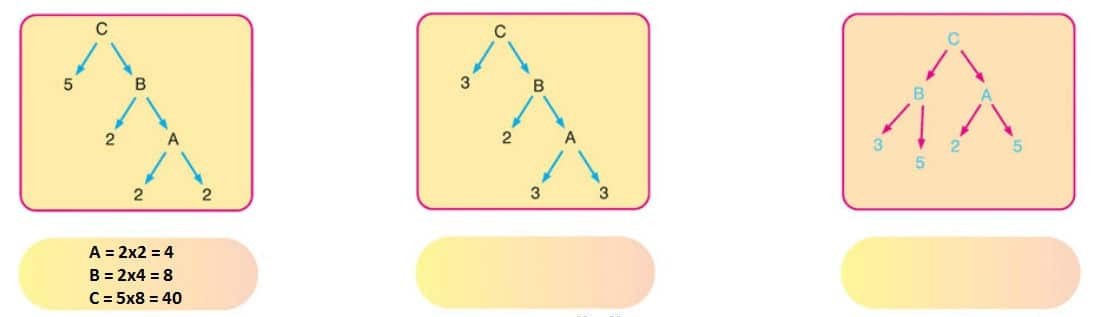
SORU: Aşağıdaki çarpan ağaçlarında verilmeyen A, B ve C sayılarını bulunuz.

ÇÖZÜM: Birinci çarpan ağacı örneğini birlikte yapalım, kalan çarpan ağacı örnekleri sizin olsun.

Çarpan ağacında her sayı altındaki sayıların çarpımına eşittir. Alttan başlayarak

A = 2.2 = 4

B = 2.4 = 8

C = 5.8 = 40 bulunur.

2) Asal Çarpanlar Algoritması (Bölen Listesi)

Bölen listesi yani diğer adıyla asal çarpanlar algoritması nedir, nasıl yapılır görelim.

Sayımızın yanına dikey bir çizgi çekeriz ve en küçük asal sayıdan başlayarak ve tam bölünmediğinde bir sonraki asal sayıya geçerek bölme işlemi yaparız. 1’i elde edince işlemimiz sona erer. Çizginin sağında kalan sayılar sayımızın asal çarpanlarıdır.

Bölen listesinde çizginin sağındaki asal sayıların çarpımı, çarpanlarına ayırdığımız sayıyı verir. Bir sayıyı bu şekilde yazarsak asal çarpanlarının tabanlarda bulunduğu üslü ifadelerin çarpımı şeklinde yazmış oluruz.

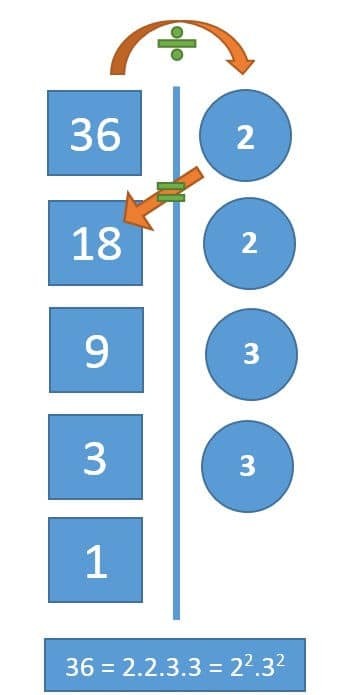
ÖRNEK: 36 sayısını bölen listesi ile asal çarpanlarına ayıralım.

36 sayısını 2’den başlayarak asal sayılara sırayla bölüyoruz.

1’i elde ettiğimizde çizginin sağ tarafında kalan sayılar 36’nın asal çarpanlarıdır.

36 sayısının asal çarpanları 2 ve 3’tür.

Çizginin sağ tarafındaki sayıları çarparak 36 sayısını elde edebiliriz.

36 sayısının asal çarpanlarının çarpımı şeklinde yazılmış hali 36 = 2² . 3² ‘dir.

SORU: Aşağıdaki bölen listelerinde verilmeyen A, B ve C sayılarını bulunuz.

ÇÖZÜM: Birinci bölen listesi örneğini birlikte yapalım, kalan bölen listesi örnekleri sizin olsun.

Bölen listesinde soldaki sayıyı sağındaki sayıya böleriz, çıkan sonucu altına yazarız. Alttan başlayarak

A : 3 = 5 olacağı için A = 15

B : 2 = 15 olacağı için B = 30

C : 2 = 30 olacağı için C = 60 bulunur.

KONUYU PEKİŞTİRMEK İÇİN: