Kareköklü Bir Sayıyı a√b Şeklinde Yazma

KAREKÖKTEN SAYI NASIL ÇIKARILIR?

Tam kare sayıları karekökten çıkarmayı Kareköklü Sayılar ve Tam Kare Sayılar konusunda anlatmıştık. Şimdi ise tam kare olmayan sayıların çarpanlarını kökten çıkarmayı öğreneceğiz.

Kareköklü bir sayıyı \(a\sqrt b\) şeklinde yazmak için karekök içindeki sayı çarpanlarından en az biri tam kare sayı olacak şekilde iki sayının çarpımı olarak yazılır. Tam kare olan çarpanların karekökleri, karekök dışına katsayı olarak yazılır.
\(a\geq0\) olmak üzere \(\sqrt{a^2.b}=a\sqrt b\) eşitliği vardır.

Karekök içindeki sayının çarpanlarından hiçbiri tam kare sayı değilse karekök dışına çıkarılamaz.

ÖRNEK: \(\sqrt{72}\) sayısını \(a\sqrt b\) şeklinde yazalım. Bu işlemi 2 farklı yolla yapabiliriz.

1. YOL: 72’yi birisi tam kare olmak şartıyla iki sayının çarpımı şeklinde kökün içine yazarız.
Tam kare olan çarpan kök dışına çıkartılır. Diğer çarpanın 1’den büyük tam kare çarpanı yoksa kök içinde kalır.

\(\sqrt{72}=\sqrt{36.2\;}=6\sqrt2\)

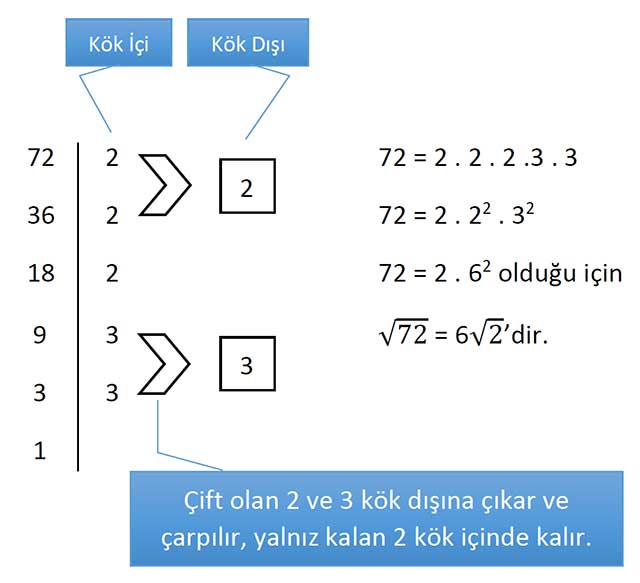
2. YOL: 72’yi asal çarpanlarına ayırırız. Eşi olan sayıları ikişerli eşleştiririz. Eşleşen bu çiftler karekök dışına çıkabilir. Sonuç olarak kök dışına çıkan sayılar çarpılarak kökün dışına, eşleşmeyen sayılar çarpılarak kökün içine yazılır.

ÖRNEK: Aşağıdaki kareköklü sayıları \(a\sqrt b\) şeklinde yazalım.

► \(\sqrt8=\sqrt{4.2}=2\sqrt2\)

► \(\sqrt{27}=\sqrt{9.3}=3\sqrt3\)

► \(\sqrt{75}=\sqrt{25.3}=5\sqrt3\)

► \(\sqrt{98}=\sqrt{49.2}=7\sqrt2\)

► \(\sqrt{200}=\sqrt{100.2}=10\sqrt2\)

KONUYU PEKİŞTİRMEK İÇİN:

ÖNCEKİ KONU	SONRAKİ KONU
Tam Kare Olmayan Sayıların Karekökleri	Kareköklü Sayılarda Katsayıyı Kök İçine Alma