BU KONUDA ÖĞRENECEKLERİMİZ:
✓ Özdeşlik Nedir?
✓ Özdeşlik ile Denklem Arasındaki Fark Nedir?
✓ Önemli Özdeşlikler
✓ Özdeşlik Modelleri
ÖZDEŞLİK NEDİR?
İçindeki değişkenlere verilen bütün gerçek sayılar için doğru olan denklemlere özdeşlik denir.
Özdeşlik mi? Özdeşlik Değil mi?
Bir ifade için “Özdeşlik mi yoksa denklem mi?” demek yanlış bir sorudur çünkü özdeşlikler de aynı zamanda denklemdir. “Bu ifade özdeşlik mi yoksa özdeşlik değil mi?” sorusu ise doğru bir sorudur ve bu sorunun cevabını bulmaya çalışalım. Özdeşlik ile özdeşlik olmayan bir denklem arasındaki fark; özdeşlikte değişkene verilen her gerçek sayı değerinde eşitlik sağlanır, özdeşlik olmayan bir denklemde ise sadece bazı gerçek sayı değerlerinde eşitlik sağlanır.
ÖRNEK: 2.(x − 2) = 2x − 4 ve 2.(x − 2) = 4 eşitliklerinde x yerine farklı değerler vererek eşitliğin sağlanıp sağlanmadığını kontrol edelim.
x yerine her iki eşitlikte de 1 yazalım
2.(x − 2) = 2x − 4
2.(1 − 2) = 2.1 − 4
−2 = −2
2.(x − 2) = 4
2.(1 − 2) = 4
−2 ≠ 4
x yerine her iki eşitlikte de 2 yazalım
2.(x − 2) = 2x − 4
2.(2 − 2) = 2.2 − 4
0 = 0
2.(x − 2) = 4
2.(2 − 2) = 4
0 ≠ 4
x yerine her iki eşitlikte de 4 yazalım
2.(x − 2) = 2x − 4
2.(4 − 2) = 2.4 − 4
4 = 4
2.(x − 2) = 4
2.(4 − 2) = 4
4 = 4
Görüldüğü gibi soldaki eşitlik x yerine yazdığımız üç değer için de sağlandı. Sağdaki eşitlik ise x yerine sadece 4 yazdığımızda sağlandı. Bu yüzden: 2.(x − 2) = 2x − 4 bir özdeşlikti, 2.(x − 2) = 4 özdeşlik değildir.
► Bir eşitliğin özdeşlik olup olmadığını anlamak için farklı değerler verip eşitliğin sağlanıp sağlanmadığına bakılabilir. Eğer verilen tüm değerler için sağlamıyorsa özdeşlik değildir.
► Bir eşitliğin özdeşlik mi denklem mi olduğunun ikinci yolu ise denklemi çözmektir. Eğer denklemi çözdükten sonra 0=0 çıkıyorsa bu denklem bir özdeşliktir.
ÖRNEK: 3x − 5 = x + 3 ve 2x + 2 = 2 + 2x eşitliklerinden özdeşlik olanlarını belirleyelim.
Önce ilk denklemi çözelim.
3x − 5 = x + 3
3x − x = 3 + 5
2x = 8
x = 4
İlk eşitlik özdeşlik değildir. (Sadece x=4 için eşitlik sağlanır.)
Şimdi ikinci denklemi çözelim.
2x + 2 = 2 + 2x
2x − 2x = 2 − 2
0 = 0
İkinci eşitlik bir özdeşliktir. (x’in her değeri için eşitlik sağlanır.)
ÖNEMLİ ÖZDEŞLİKLER
Tam Kare Özdeşliği – İki Terimin Toplamının Karesi
İki terimin toplamının karesi, bu iki terimin kareleri ve bu iki terimin çarpımının iki katının toplamına eşittir.
(a + b)2 = a2 + 2ab + b2
ÖRNEK: Bu özdeşliği şu şekilde kullanabiliriz. 102’nin karesini bu özdeşlik sayesinde şu şekilde bulabiliriz.
(100 + 2)2 = 1002 + 2.100.2 + 22
(100 + 2)2 = 10000 + 400 + 4
(100 + 2)2 = 10404
Tam Kare Özdeşliği – İki Terimin Toplamının Karesini Modelleme
Birinci şekildeki karenin alanı, parçaların alanları toplamına eşittir.

Tam Kare Özdeşliği – İki Terimin Farkının Karesi
İki terimin farkının karesi, bu iki terimin kareleri toplamından bu iki terimin çarpımının iki katının çıkarılmasına eşittir.
(a − b)2 = a2 − 2ab + b2
ÖRNEK: Bu özdeşliği şu şekilde kullanabiliriz. 97’nin karesini bu özdeşlik sayesinde şu şekilde bulabiliriz.
(100 − 3)2 = 1002 − 2.100.3 + 32
(100 − 3)2 = 10000 − 600 + 9
(100 − 3)2 = 9409
Tam Kare Özdeşliği – İki Terimin Farkının Karesinin Modelleme
Birinci şekildeki yeşil karenin alanı, büyük karenin alanından beyaz bölgelerin alanlarının çıkarılmasına eşittir.

İki Kare Farkı Özdeşliği
İki terimin karelerinin farkı, bu iki terimin toplamı ile farkının çarpımına eşittir.
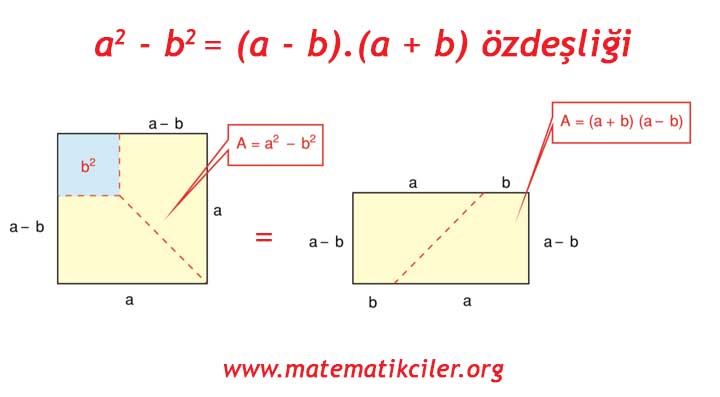
a2 − b2 = (a − b) . (a + b)
ÖRNEK: Bu özdeşliği şu şekilde kullanabiliriz. 75’in karesi ile 25’in karesinin farkını bu özdeşlik sayesinde şu şekilde bulabiliriz.
752 − 252 = (75 − 25) . (75 + 25)
752 − 252 = 50 . 100
752 − 252 = 5000
İki Kare Farkı Özdeşliğini Modelleme
Birinci şekildeki büyük kareyle küçük karenin alanları farkı (sarı bölge), ikinci şekildeki sarı bölgeye eşittir.
BİR KAÇ ÖNEMLİ ÖZDEŞLİK
- İKİ KARE FARKI
a2 − b2 = (a − b) . (a + b)
- İKİ KARE TOPLAMI
a2 + b2 = (a − b)2 + 2ab
a2 + b2 = (a + b)2 − 2ab
- TAM KARE İFADELER
(a + b)2 = a2 + 2ab + b2
(a − b)2 = a2 − 2ab + b2
(a + b)2 = (a − b)2 + 4ab
(a − b)2 = (a + b)2 − 4ab
- İKİ KÜP FARKI
a3 − b3 = (a − b) . (a2 + ab + b2)
a3 + b3 = (a + b) . (a2 − ab + b2)
a3 − b3 = (a − b)3 + 3ab . (a − b)
a3 + b3 = (a + b)3 − 3ab . (a + b)
- KÜP AÇILIMI
(a + b)3 = a3 + 3a2b + 3ab2 + b3
(a − b)3 = a3 − 3a2b + 3ab2 − b3
KONUYU PEKİŞTİRMEK İÇİN:
İLGİLİ ÇALIŞMA KAĞIDI BAĞLANTISI
İLGİLİ KAZANIM TESTİ BAĞLANTISI
TEST ÇÖZME BAĞLANTISI
KONU KAZANIMLARI
BU KONUYLA İLGİLİ KAZANIMLAR:
✓ Özdeşlikleri modellerle açıklar.
| ÖNCEKİ KONU | SONRAKİ KONU |
| Cebirsel İfadeler | Cebirsel İfadeleri Çarpanlara Ayırma |
