EN BÜYÜK ORTAK BÖLEN (EBOB)
En az biri sıfırdan farklı iki veya daha fazla tam sayının pozitif ortak bölenlerinin en büyüğüne bu sayıların en büyük ortak böleni kısaca “EBOB“u denir.
a ve b tam sayılarının en büyük ortak böleni EBOB(a,b) veya (a,b)ebob şeklinde gösterilir.
ÖRNEK: 18 ve 24 sayılarının en büyük ortak bölenini adım adım bulalım.
► Öncelikle 18 ve 24 sayılarının pozitif bölenlerini yazalım ve ortak olanları işaretleyelim.
18’in pozitif tam sayı bölenleri:
1, 2, 3, 6, 9, 18
24’ün pozitif tam sayı bölenleri:
1, 2, 3, 4, 6, 8, 12, 24
► Ortak bölenlerin en büyüğü olan 6 bu iki sayının EBOB’udur.
EBOB (18,24) = 6 veya (18,24)ebob = 6 şeklinde gösterilir.
ÖRNEK: 18 ve 12 sayılarının EBOB’unu asal çarpanlar algoritması yöntemiyle bulalım.

Bu yöntemde sayılar yan yana yazılarak asal sayılara bölünür. Tercihen en küçük asal sayıdan başlanarak devam edilir. Asal sayı hiç bir sayıyı bölmüyorsa bir büyük asal sayıya geçilir. İki sayı da 1 olana kadar işleme devam edilir. Sayıları ortak bölen asal sayıların çarpımı bu sayıların EBOB’udur.
Verilen algoritmada 2 ve 3 sayıları hem 18’i hem de 12’yi böldükleri için işaretlenmiştir. İşaretli sayıların çarpımı EBOB’u verir.
EBOB (18, 12) = 2.3 = 6
EN KÜÇÜK ORTAK KAT (EKOK)
En az biri sıfırdan farklı iki veya daha fazla tam sayının pozitif ortak katlarının en küçüğüne bu sayıların en küçük ortak katı kısaca “EKOK“u denir.
a ve b tam sayılarının en küçük ortak katı EKOK(a,b) veya (a,b)ekok şeklinde gösterilir.
ÖRNEK: 4 ve 6 sayılarının en küçük ortak katını adım adım bulalım.
► Öncelikle 4 ve 6 sayılarının pozitif katlarını yazalım ve ortak olanları işaretleyelim.
4’ün pozitif tam katları:
4, 8, 12, 16, 20, 24, 28, …
6’nın pozitif tam katları:
6, 12, 18, 24, 30, 36, 42, …
► Ortak katların en küçüğü olan 12 bu iki sayının EKOK’udur.
EKOK (4,6) = 12 veya (4,6)ekok = 12 şeklinde gösterilir.
ÖRNEK: 18 ve 12 sayılarının EKOK’unu asal çarpanlar algoritması yöntemiyle bulalım.
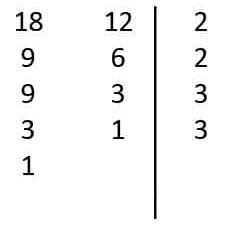
Bu yöntemde sayılar yan yana yazılarak asal sayılara bölünür. Tercihen en küçük asal sayıdan başlanarak devam edilir. Asal sayı hiç bir sayıyı bölmüyorsa bir büyük asal sayıya geçilir. İki sayı da 1 olana kadar işleme devam edilir. Sayıları bölen tüm asal sayıların çarpımı bu sayıların EKOK’udur.
Verilen algoritmada sayıları bölen asal sayılar 2, 2, 3,3 olarak görülmektedir. Bu sayıların çarpımı EKOK’u verir.
EKOK (18, 12) = 2.2.3.3 = 36
EBOB ve EKOK’UN ÖZELLİKLERİ
İki pozitif tam sayının çarpımı, bu sayıların EBOB’u ile EKOK’unun çarpımına eşittir.
a ve b pozitif tam sayıları için, a . b = EBOB (a,b) . EKOK (a,b)
ÖRNEK: 6 ve 8 sayılarını inceleyelim:
6 ve 8 sayılarının EBOB’u 2, EKOK’u 24’tür.
Burada 6 . 8 = 2 . 24 eşitliğinin sağlandığı görülür.
Biri diğerinin tam katı olan iki pozitif tam sayının EBOB’u küçük sayıya, EKOK’u büyük sayıya eşittir.
a sayısı b’nin tam katı ise, EBOB (a,b) = b ve EKOK (a,b) = a
ÖRNEK: 6 ve 12 sayılarını inceleyelim:
6 ve 12 sayılarının EBOB’u 6, EKOK’u 12’dir.
Burada EBOB’un küçük sayıya, EKOK’un büyük sayıya eşit olduğu görülür.
Aralarında asal iki pozitif tam sayının EBOB’u 1’e, EKOK’u ise bu sayıların çarpımına eşittir.
a ve b aralarında asal ise, EBOB (a,b) = 1 ve EKOK (a,b) = a.b
ÖRNEK: 9 ve 16 sayılarını inceleyelim:
9 ve 16 sayıları aralarında asaldır, bu sayıların EBOB’u 1, EKOK’u ise 144’tür.
Burada EBOB’un 1’e, EKOK’un ise bu iki sayının çarpımına eşit olduğu görülür.
Asal çarpanlarına ayrılmış olan pozitif tam sayıların EBOB ve EKOK’u şu şekilde bulunur:
EBOB = Ortak olan asal çarpanlardan üssü küçük olanların çarpımı
EKOK = Ortak olan asal çarpanlardan üssü büyük olanlar ile ortak olmayan asal çarpanların çarpımı
ÖRNEK: A = 2. 3 . 53 ve B = 22 . 3 . 52 . 7 sayılarını inceleyelim:
Ortak olan asal çarpanlardan üssü küçük olanlar (aşağıda kalın yazılmıştır) EBOB’a, diğerleri EKOK’a yazılır ve çarpılır.
A = 21 . 31 . 53
B = 22 . 31 . 52 . 7
EBOB (A,B) = 21 . 31 . 52
EKOK (A,B) = 22 . 31 . 53 . 7
EBOB – EKOK SORULARI
► 20, 30 ve 50 sayılarının EBOB ve EKOK’larını bulalım.

EBOB (20, 30, 50) = 2.5 = 10
EKOK (20, 30, 50) = 2.2.3.5.5 = 300
► EBOB (23, 69) + EKOK (23, 69) işleminin sonucunu bulalım.
69 sayısı 23’ün tam katı olduğu için bu sayıların EBOB’u 23, EKOK’u 69’dur.
Sonuç 23 + 69 = 92 olarak bulunur.
► 20 ile A sayısının EBOB’u 10, EKOK’u 60 ise A sayısını bulalım.
İki sayının çarpımı, bu sayıların EBOB’u ile EKOK’unun çarpımına eşittir.
Bu yüzden 20.A = 10.60 eşitliğinden A = 30 olarak bulunur.
► 24 ile 25 sayılarının EBOB ve EKOK’unu bulalım.
Ardışık sayılar aralarında asaldır ve aralarında asal sayıların EBOB’u 1, EKOK’u sayıların çarpımıdır.
Bu yüzden EBOB (24,25) = 1 ve EKOK (24,25) = 600 olarak bulunur.
► K = 23 . 32 . 5 , L = 22 . 32 . 7 ve M = 24 . 3 ise EBOB (K, L, M) ve EKOK (K, L, M) değerlerini bulalım.
Ortak olan asal çarpanlardan üssü küçük olanlar EBOB’a, üssü büyük olanlar ile ortak olmayanlar EKOK’a yazılır ve çarpılır.
K = 23 . 32 . 5
L = 22 . 32 . 7
M = 24 . 31
EBOB (K, L, M) = 22 . 3
EKOK (K, L, M) = 24 . 32 . 5 . 7
EBOB – EKOK PROBLEMLERİ
“EBOB ve EKOK problemleri nasıl çözülür?” sorusunun cevabı “EBOB – EKOK problemleri nasıl ayırt edilir?” sorusunun cevabında gizlidir. Öncelikle soruda verilenler ile istenilene nasıl ulaşılabileceği düşünülürse soruda EBOB mu EKOK mu kullanılacak ortaya çıkmış olur. Eğer istenilene ulaşırken verilen sayıların katları kullanılacak ise EKOK, bölenleri kullanılacak ise EBOB çözüme yardımcı olacaktır.
EBOB – EKOK sorularını ayırt etmede her soruda geçerli bir kural yoktur ancak genel olarak şu şekilde ayırt edilebilir:
- PARÇA verilip BÜTÜN soruluyorsa EKOK kullanılır.
- BÜTÜN verilip PARÇA soruluyorsa EBOB kullanılır.
EBOB SORULARI GENELDE ŞÖYLEDİR:
1) Bidonlarda, varillerde, şişelerde, çuvallarda, kaplarda bulunan malzemeler verilip daha küçük eşit başka kaplara aktarılıyorsa,
2) Tarlanın, bahçenin, arsanın ölçüleri verilip etrafına eşit aralıklarla ağaç veya direk dikiliyorsa,
3) Gruplar verilip bunlar için kaç uçak, otobüs, araba veya oda gerekir diye soruluyorsa,
4) Dikdörtgenler prizması şeklindeki odanın, kutunun, deponun ölçüleri verilip içine kaç küp sığar diye soruluyorsa,
5) Kumaşlar, bezler, demir çubukların uzunlukları verilip eşit parçalara ayrılıyorsa,
6) Dikdörtgen şeklindeki kartonun ölçüleri verilip küçük kare kartonlara parçalanıyorsa EBOB kullanılır.
EKOK SORULARI GENELDE ŞÖYLEDİR:
1) Cevizler, fındıklar, şekerler, bilyeler üçer-beşer vs. sayılıyorsa veya bunlar sayıldıktan sonra artan oluyorsa,
2) Gemiler, arabalar, yarışçılar beraber yola çıkıp bir yerde karşılaşıyorsa,
3) Sınıfta öğrenciler ikişer-üçer vs. sıralara oturuyorlarsa veya bunlardan ayakta kalanlar oluyorsa,
4) Ziller, saatler birlikte ne zaman çalar diye soruluyorsa,
5) Doktorlar, hemşireler, işçiler birlikte ne zaman nöbet tutar diye soruluyorsa,
6) Dikdörtgenler prizması şeklindeki tuğlaların, kutuların ölçüleri verilip küp yapılıyorsa EKOK kullanılır.
ÇÖZÜMLÜ PROBLEMLER
► 80 cm ve 120 cm uzunluğunda iki demir çubuk, hiç artmadan eşit uzunlukta parçalara ayrılacaktır. Bir parçanın uzunluğu en fazla kaç cm olur?
Bütün verilip eş parçalara ayrılacağı için EBOB kullanılır.
EBOB (80, 120) = 40 cm olarak cevap bulunur.
► 40 L zeytin yağı ve 70 L ayçiçek yağı hiç artmadan eşit hacimli şişelere doldurulacaktır. Bu iş için en az kaç şişe gereklidir?
Bütün verilip eş parçalara ayrılacağı için EBOB kullanılır. Az şişe kullanmak için şişenin hacminin büyük olması gerekir.
EBOB (40, 70) = 10 L (şişenin hacmi)
40 : 10 = 4 şişe zeytin yağı, 70 : 10 = 7 şişe ayçiçek yağı olur. Toplam 11 şişe gereklidir.
► Yunus bilyelerini dörder, beşer ve altışar saydığında her defasında 1 bilyesi artıyor. Buna göre, Yunus’un en az kaç tane bilyesi vardır?
Eğer 1 bilyesi eksik olsaydı bilye sayısı hem 4’ün, hem 5’in, hem de 6’nın katı olacaktı.
EKOK (4, 5, 6) = 60 bilye 4, 5 ve 6’ya bölünür.
Ancak 1 bilyesi eksik olsaydı diye düşündüğümüz için en az 61 bilyesi vardır.
► Doktor Ayşe 6 günde bir, hemşire Zeynep 8 günde bir nöbet tutmaktadır. İkisi birlikte Cuma günü nöbet tuttuktan sonraki 2. birlikte nöbetleri hangi gün olur?
EKOK (6, 8) = 24 gün
Cuma’dan sonraki → ilk nöbet 24 gün sonra → 2. nöbet 48 gün sonra
Haftanın günleri 7 günde tekrarlar. 49 gün sonra Cuma olacağı için 48 gün sonrası Perşembe olur.
| ÖNCEKİ KONU | SONRAKİ KONU |
| Bölünebilme Kuralları | Periyodik Olarak Tekrar Eden Durumlar |
matematikciler.com olarak ziyaretçilerimize ücretsiz ve nitelikli içerikler sunmak için yoğun çaba sarfediyoruz. Bu emeğin korunması adına bu konu anlatımının izinsiz yayınlanması yasaktır!
