Kartezyen Çarpım

SIRALI İKİLİ

a ve b gibi iki eleman arasına virgül konularak (a, b) şeklinde yazılmasına sıralı ikili denir. (a, b) sıralı ikilisinde a’ya birinci bileşen, b’ye ikinci bileşen denir.

ÖRNEK: Aşağıdaki kişilerin konumlarını ilk bileşen sütun olacak şekilde sıralı ikili olarak gösterelim.

	1	2	3	4
1			Ece
2	Ali
3		Nil
4				Can

Sıralı ikililer Ece (3, 1) – Ali (1, 2) – Nil (2, 3) – Can (4, 4) şeklinde olur.

Sıralı ikililerde bileşenlerin sırası önemlidir. (a, b) \(\neq\) (b, a)

Sıralı İkililerin Eşitliği

İki sıralı ikilinin birinci bileşenleri birbirlerine, ikinci bileşenleri de birbirlerine eşit ise bu sıralı ikiler eşittir.

(a, b) ve (c, d) sıralı ikilileri birbirine eşit ise bu durum (a, b) = (c, d) şeklinde gösterilir. Bu durumda a = c ve b = d olur.

ÖRNEK: (2x + 1 , 9) = (11, 3y) olduğuna göre x + y kaçtır bulalım.

Eşit sıralı ikililerde aynı sıradaki bileşenler birbirine eşittir.

2x + 1 = 11 olur ve buradan x = 5 bulunur.

9 = 3y olur ve buradan y = 3 bulunur.

x + y = 5 + 3 = 8 olarak sonuç bulunur.

KARTEZYEN ÇARPIM KÜMESİ

Birinci bileşeni bir A kümesinden, ikinci bileşeni ise bir B kümesinden alınarak oluşturulan tüm sıralı ikililerin kümesine A kartezyen çarpım B kümesi denir ve AxB şeklinde gösterilir.

AxB kümesinin ortak özellik yöntemi ile AxB = { (a, b) | a \(\in\) A ve b \(\in\) B} şeklinde ifade edilir.

ÖRNEK: A = {a, b, c} ve B = {1, 2} kümeleri verilsin. AxB ve BxA kümelerini yazalım.

► AxB kümesini yazmak için A’daki elemanların her birini B’dekilerle tek tek eşleştirip yazalım.

AxB = {(a, 1), (a, 2), (b, 1), (b, 2), (c, 1), (c, 2)} olur.

► BxA kümesini yazmak için B’deki elemanların her birini A’dakilerle tek tek eşleştirip yazalım.

BxA = {(1, a), (1, b), (1, c), (2, a), (2, b), (2, c)} olur.

KARTEZYEN ÇARPIM KÜMESİNİN GRAFİĞİ

Kartezyen çarpım grafiği çizilirken kartezyen çarpım kümesinin elemanları birinci bileşenleri x ekseninde, ikinci bileşenleri y ekseninde olacak şekilde işaretlenir.

ÖRNEK: A = {2, 3} ve B = {1, 2, 3} kümeleri verilsin. AxB kümesini bulalım ve grafiğini çizelim.

AxB = {(2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3)}

x ekseni A, y ekseni B olacak şekilde grafik çizilir.

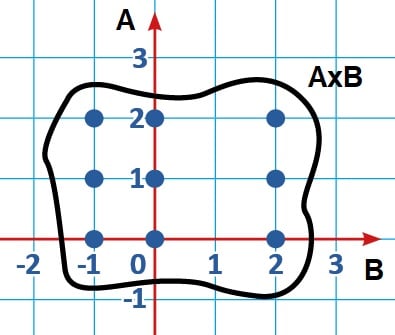
ÖRNEK: A = {0, 1, 2} ve B = {−1, 0, 2} kümeleri verilsin. BxA kümesini bulalım ve grafiğini çizelim.

BxA = {(−1, 0), (−1, 1), (−1, 2), (0, 0), (0, 1), (0, 2), (2, 0), (2, 1), (2, 2)}

x ekseni B, y ekseni A olacak şekilde grafik çizilir.

KARTEZYEN ÇARPIMIN ÖZELLİKLERİ

1) AxB \(\neq\) BxA

Kartezyen çarpımda değişme özelliği yoktur.

2) Ax\(\varnothing\) = \(\varnothing\)xA = \(\varnothing\)

Bir kümenin boş küme ile kartezyen çarpımı boş kümedir.

3) s(AxB) = s(A) . s(B)

A ile B’nin kartezyen çarpım kümesinin eleman sayısı, bu kümelerin eleman sayıları çarpımına eşittir.

4) Ax(B \(\cap\) C) = (AxB) \(\cap\) (AxC)

Kartezyen çarpımın kesişim üzerine dağılma özelliği vardır.

5) Ax(B \(\cup\) C) = (AxB) \(\cup\) (AxC)

Kartezyen çarpımın birleşim üzerine dağılma özelliği vardır.

ÖNCEKİ KONU	SONRAKİ KONU
Kümelerde İşlemler	Sayı Kümeleri