KÜMELERDE KESİŞİM VE BİRLEŞİM İŞLEMİ
A ve B gibi iki kümenin ortak elemanlarından oluşan kümeye A ile B’nin kesişim kümesi denir ve A \(\cap\) B biçiminde gösterilir.
A ve B kümelerinin kesişimi ortak özellik yöntemi ile A \(\cap\) B = { x | x \(\in\) A ve x \(\in\) B } şeklinde ifade edilir.

A ve B kümelerinin kesişim kümesi, Venn şeması ile aşağıdaki gibi gösterilir.
ÖRNEK: Aşağıdaki kümelerin kesişim kümelerini bulalım.
► A = { 1, 2, 3, 4 } ve B = { 3, 4, 5, 6, 7 }
A \(\cap\) B = { 3, 4 }
► K = { a, b, c } ve L = { k, l, m, n, p }
K \(\cap\) L = { }
► P = { 1, 2, 3, 4 }, R = { 4, 5, 6 } ve S = { 2, 4, 6, 8 }
P \(\cap\) R \(\cap\) S = { 4 }
A ve B gibi iki kümenin bütün elemanlarından oluşan kümeye A ile B’nin birleşim kümesi denir ve A \(\cup\) B biçiminde gösterilir.
A ve B kümelerinin birleşimi ortak özellik yöntemi ile A \(\cup\) B = { x | x \(\in\) A veya x \(\in\) B } şeklinde ifade edilir.
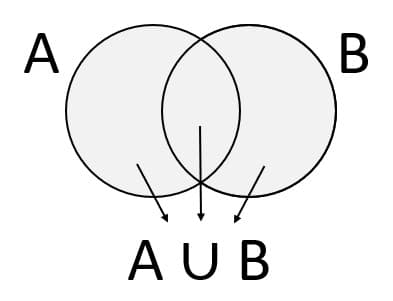
A ve B kümelerinin birleşim kümesi, Venn şeması ile aşağıdaki gibi gösterilir.
ÖRNEK: Aşağıdaki kümelerin birleşim kümelerini bulalım.
► A = { 1, 2, 3, 4 } ve B = { 3, 4, 5, 6, 7 }
A \(\cup\) B = { 1, 2, 3, 4, 5, 6, 7 }
► K = { a, b, c } ve L = { k, l, m }
K \(\cup\) L = { a, b, c, k, l, m }
► P = { 1, 2, 3, 4 }, R = { 4, 5, 6 } ve S = { 2, 4, 6, 8 }
P \(\cup\) R \(\cup\) S = { 1, 2, 3, 4, 5, 6, 8 }
ÖRNEK: Aşağıdaki kümelerin kesişim ve birleşim kümelerini bulalım.

P \(\cap\) R = { E, İ }
P \(\cup\) R = { C, L, E, İ, N, S, B }
NOT: İki kümenin birleşiminin eleman sayısı, kümelerin eleman sayıları toplamından kesişimlerinin eleman sayısı çıkarılarak bulunur.
s(A \(\cup\) B) = s(A) + s(B) − s(A \(\cap\) B)
s(P \(\cup\) R) = s(P) + s(R) − s(P \(\cap\) R)
s(P \(\cup\) R) = 4 + 5 − 2 = 7
ÖRNEK: Aşağıdaki kümelerin kesişim ve birleşim kümelerini bulalım.

S \(\cap\) M = M = { 7, 51 }
S \(\cup\) M = S = { 7, 51, 12, 30 }
NOT: Biri diğerinin alt kümesi olan iki kümenin kesişimi kapsanan kümeye, birleşimi kapsayan kümeye eşittir.
A \(\subset\) B ise s(A \(\cap\) B) = s(A) ve s(A \(\cup\) B) = s(B) olur.
s(M \(\cap\) S) = s(M) = 2
s(M \(\cup\) S) = s(S) = 4
ÖRNEK: Aşağıdaki kümelerin kesişim ve birleşim kümelerini bulalım.

K \(\cap\) L = { }
K \(\cup\) L = { 3, 5, 7, 0, 4, 8 }
NOT: Kesişimleri boş küme olan kümelere ayrık kümeler denir. Ayrık iki kümenin birleşiminin eleman sayısı, kümelerin eleman sayıları toplamına eşittir.
A ve B ayrık kümeler ise s(A \(\cup\) B) = s(A) + s(B) olur.
s(K \(\cup\) L) = s(K) + s(L)
s(K \(\cup\) L) = 3 + 3 = 6
Kesişim ve Birleşim İşlemlerinin Özellikleri
1) TEK KUVVET ÖZELLİĞİ
Kesişim işleminin tek kuvvet özelliği vardır.
A \(\cap\) A = A
Birleşim işleminin tek kuvvet özelliği vardır.
A \(\cup\) A = A
2) DEĞİŞME ÖZELLİĞİ
Kesişim işleminin değişme özelliği vardır.
A \(\cap\) B = B \(\cap\) A
Birleşim işleminin değişme özelliği vardır.
A \(\cup\) B = B \(\cup\) A
3) BİRLEŞME ÖZELLİĞİ
Kesişim işleminin birleşme özelliği vardır.
A \(\cap\) ( B \(\cap\) C ) = ( A \(\cap\) B ) \(\cap\) C
Birleşim işleminin birleşme özelliği vardır.
A \(\cup\) ( B \(\cup\) C ) = ( A \(\cup\) B ) \(\cup\) C
4) YUTAN VE BİRİM ELEMAN
Kesişim işleminin yutan elemanı boş kümedir.
A \(\cap\) \(\varnothing\) = \(\varnothing\)
Birleşim işleminin etkisiz elemanı boş kümedir.
A \(\cup\) \(\varnothing\) = A
5) DAĞILMA ÖZELLİĞİ
Kesişim işleminin birleşim üzerine soldan ve sağdan dağılma özelliği vardır.
A \(\cap\) ( B \(\cup\) C ) = ( A \(\cap\) B ) \(\cup\) ( A \(\cap\) C )
( B \(\cup\) C ) \(\cap\) A = ( B \(\cap\) A ) \(\cup\) ( C \(\cap\) A )
Birleşim işleminin kesişim üzerine soldan ve sağdan dağılma özelliği vardır.
A \(\cup\) ( B \(\cap\) C ) = ( A \(\cup\) B ) \(\cap\) ( A \(\cup\) C )
( B \(\cap\) C ) \(\cup\) A = ( B \(\cup\) A ) \(\cap\) ( C \(\cup\) A )
KÜMELERDE FARK İŞLEMİ
A ve B herhangi iki küme olmak üzere A kümesinde olup B kümesinde olmayan tüm elemanların oluşturduğu kümeye A kümesinin B kümesinden farkı denir. A − B ya da A \ B ile gösterilir.
A kümesinin B kümesinden farkı ve B kümesinin A kümesinden farkı ortak özellik yöntemi ile
A \ B = { x | x \(\in\) A ve x \(\notin\) B } ve B \ A = { x | x \(\in\) B ve x \(\notin\) A } şeklinde ifade edilir.
A ve B kümelerinin birbirlerinden farkı, Venn şeması ile aşağıdaki gibi gösterilir.

ÖRNEK: Aşağıdaki kümelerin birbirinden farklarını bulalım.
► A = { 1, 2, 3, 4 } ve B = { 3, 4, 5 }
A \ B = { 1, 2 }
B \ A = { 5 }
► K = { a, b, c } ve L = { ğ, ş }
K \ L = K = { a, b, c }
L \ K = L = { ğ, ş }
NOT: Ayrık iki kümede bir kümenin diğerinden farkı kendisine eşittir. A \ B = A ve B \ A = B
Fark İşleminin Özellikleri
1) A \(\neq\) B ise A \ B \(\neq\) B \ A olur.
Fark işleminde değişme özelliği yoktur.
2) A \ A = \(\varnothing\)
Bir kümenin kendisinden farkı boş kümedir.
3) A \ \(\varnothing\) = A
Bir kümenin boş kümeden farkı kendisidir.
4) A \ E = \(\varnothing\)
Bir kümenin evrensel kümeden farkı boş kümedir.
BİR KÜMENİN TÜMLEYENİ
E evrensel küme olmak üzere A kümesinde olmayan elemanların oluşturduğu kümeye A kümesinin tümleyeni denir ve A’ ile gösterilir.
A’nın tümleyen kümesi A’ ortak özellik yöntemi ile A’ = { x | x \(\notin\) A ve x \(\in\) E } şeklinde ifade edilir.
ÖRNEK: Aşağıda Evrensel küme içerisinde verilen A kümesini inceleyelim.

► A’ = { 0, 4 }
► ( A’ )’ = { 1, 2, 3 } = A
► A \(\cap\) A’ = \(\varnothing\)
► A \(\cup\) A’ = { 0, 1, 2, 3, 4 } = E
► s(A) \(\cup\) s(A’) = 3 + 2 = 5 = s(E)
► E \ A = { 0, 4 } = A’
► E’ = \(\varnothing\)
Şimdi bu örnekten yola çıkarak tümleyenin özelliklerini yazalım.
Tümleme ile İlgili Özellikler
1) ( A’ )’ = A
Bir kümenin tümleyeninin tümleyeni kendisidir.
2) A \(\cap\) A’ = \(\varnothing\)
Bir kümenin tümleyeni ile kesişimi boş kümedir.
3) A \(\cup\) A’ = E
Bir kümenin tümleyeni ile birleşimi evrensel kümedir.
4) s(A) \(\cup\) s(A’) = s(E)
Bir kümenin eleman sayısı ile tümleyeninin eleman sayısının toplamı evrensel kümenin eleman sayısına eşittir.
5) E \ A = A’
Evrensel kümenin bir kümeden farkı o kümenin tümleyenidir.
6) E’ = \(\varnothing\)
Evrensel kümenin tümleyeni boş kümedir.
7) \(\varnothing\)‘ = E
Boş kümenin tümleyeni evrensel kümedir.
NOT: Aşağıda önemli eşitlikler verilmiştir. Bu eşitliklerin doğruluğunu Venn şeması çizerek kolayca görebilirsiniz.
A \ B = A \(\cap\) B’ ve B \ A = B \(\cap\) A’
DE MORGAN KURALLARI
Sembolik mantıkta olduğu gibi kümelerde de De Morgan kuralları bulunur.
(A \(\cup\) B)’ = A’ \(\cap\) B’
(A \(\cap\) B)’ = A’ \(\cup\) B’
şeklinde verilen kurallara De Morgan Kuralları denir.
KÜMELER İLE SEMBOLİK MANTIK ARASINDAKİ İLİŞKİ
Kümeler ile sembolik mantık arasındaki ilişkilerin bazıları aşağıdaki tabloda verilmiştir.
| SEMBOLİK MANTIK | KÜMELER |
|---|---|
| 0 | \(\varnothing\) |
| 1 | E |
| ∧ | \(\cap\) |
| ∨ | \(\cup\) |
| Değili (‘) | Tümleyeni (‘) |
| \(\equiv\) | = |
| (p’)’ \(\equiv\) p | (A’)’ = A |
| p ∧ p’ \(\equiv\) 0 | A \(\cap\) A’ = \(\varnothing\) |
| p ∨ p’ \(\equiv\) 1 | A \(\cup\) A’ = E |
| 1 ∧ 0 \(\equiv\) 0 | E \(\cap\) \(\varnothing\) = \(\varnothing\) |
| 1 ∨ 0 \(\equiv\) 1 | E \(\cup\) \(\varnothing\) = E |
| (p ∧ q)’ \(\equiv\) p’ ∨ q’ | (A \(\cap\) B)’ = A’ \(\cup\) B’ |
| (p ∨ q)’ \(\equiv\) p’ ∧ q’ | (A \(\cup\) B)’ = A’ \(\cap\) B’ |
| p ∧ (q ∨ r) \(\equiv\) (p ∧ q) ∨ (p ∧ r) | A \(\cap\) ( B \(\cup\) C ) = ( A \(\cap\) B ) \(\cup\) ( A \(\cap\) C ) |
| p ∨ (q ∧ r) \(\equiv\) (p ∨ q) ∧ (p ∨ r) | A \(\cup\) ( B \(\cap\) C ) = ( A \(\cup\) B ) \(\cap\) ( A \(\cup\) C ) |
| ÖNCEKİ KONU | SONRAKİ KONU |
| Kümeler | Kartezyen Çarpım |
matematikciler.com olarak ziyaretçilerimize ücretsiz ve nitelikli içerikler sunmak için yoğun çaba sarfediyoruz. Bu emeğin korunması adına bu konu anlatımının izinsiz yayınlanması yasaktır!
