Kümeler

KÜME KAVRAMI

Küme Nedir?

İyi tanımlanmış birbirinden farklı nesneler topluluğuna küme denir. Kümeler A, B, C gibi büyük harflerle isimlendirilir.

Tanımdaki iyi tanımlanmış, herkes tarafından aynı şekilde bilinen, belirli olan nesneler demektir. Örneğin “iyi insanlar” küme belirtmez çünkü iyi insanlar herkes için aynı değildir. Daha fazla örnek aşağıdaki tabloda verilmiştir.

Küme Belirtmez	Küme Belirtir
Çalışkan öğrenciler Uzun boylu insanlar Bazı hayvanlar Birkaç gün	Takdir alan öğrenciler Boyu 1,5 metreden uzun öğrenciler Uçan hayvanlar Z harfi ile başlayan aylar

Eleman ve Eleman Sayısı

Kümeyi oluşturan her nesneye o kümenin elemanı denir. Elemanıdır sembolü ∈ ile gösterilir. Elemanı değildir sembolü ∉ ile gösterilir. Bir A kümesinin eleman sayısı sembolle s(A) şeklinde gösterilir.

ÖRNEK: A kümesi haftanın P harfi ile başlayan günleri olsun.

Pazar A kümesinin elemanıdır. → Pazar ∈ A

Salı A kümesinin elemanı değildir. → Salı ∉ A

A kümesinin eleman sayısı 3′ tür. → s(A) = 3

KÜMELERİN GÖSTERİLİŞİ

Liste Yöntemi

Kümeye ait elemanların küme parantezi yani “{ }” şekli içerisine aralarına virgül konularak yazılmasına liste yöntemi denir. Kümenin her bir elemanı yalnızca bir kez yazılır ve elemanların yerinin değiştirmesi yeni bir küme oluşturmaz.

ÖRNEK: Rakamlar kümesini liste yöntemiyle yazalım.

Rakamlar kümesini R harfiyle isimlendirecek olursak R = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 0 }

ÖRNEK: MATEMATİK kelimesinin harflerini liste yöntemiyle yazalım.

Bu kümeyi M harfiyle isimlendirecek olursak M = { M, A, T, E, İ, K }

ÖRNEK: H = { #, AA, 2, 34 } kümesinin elemanlarını belirleyelim.

H kümesi 4 elemanlıdır. Bunlar #, AA, 2 ve 34’tür.

Ortak Özellik Yöntemi

Kümeye ait elemanların tek tek yazılmak yerine ortak özelliklerinin yazılmasına ortak özellik yöntemi denir. Ortak özellik yöntemiyle kümelerin gösterimi şu şekildedir: { x | x’lerin ortak özelliği }
Öyle ki anlamına gelen “ | ” sembolü yerine “ : ” sembolü de kullanılabilir.

ÖRNEK: Aşağıda liste yöntemiyle verilen kümeleri ortak özellik yöntemiyle yazalım.

► A = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 }

► B = { a, b, c, ç }

► C = { 10, 11, 12, 13 }

Kümeler ortak özellik yöntemiyle farklı şekillerde de yazılabilir. Önemli olan yazılan kümenin tam olarak (ne eksik ne fazla) kümenin elemanlarını belirtmesidir.

► A = { x | x, bir rakam }

► B = { x : x, Alfabemizin ilk dört harfinden biri }

► C = { x : 9 < x < 14 , x bir doğal sayı }

Venn Şeması

Kümeye ait elemanların kapalı bir eğri içerisinde ve her elemanın başına bir nokta konularak gösterilmesine Venn şeması yöntemi denir.

ÖRNEK: A = { a, b, c } kümesini Venn şemasıyla gösterelim.

KÜMELER

Boş Küme

Hiç bir elemanı olmayan kümeye boş küme denir. Boş küme { } ya da \(\varnothing\) sembolleri ile gösterilir..

ÖRNEK: Ç harfiyle başlayan aylar kümesine A kümesi dersek A kümesi boş küme olur.

Bu durum A = { } ya da A = \(\varnothing\) şeklinde gösterilir ve s(A) = 0 olur.

NOT: { \(\varnothing\) } ve { 0 } kümeleri boş küme olmayıp birer elemana sahip kümelerdir.

Evrensel Küme

Üzerinde işlem yapılan tüm kümelere ait elemanları içinde bulunduracak şekilde seçilen kümeye evrensel küme denir. Evrensel küme E harfi ile gösterilir.

ÖRNEK: A = { 1, 2, 3 } ve B = { 5, 12 } kümeleri için evrensel kümeler yazalım.

► E = { 1, 2, 3, 4, 5, 6, 7, 12 }

► E = { x | x, bir doğal sayı }

► E = { x | 0 < x < 20 , x bir tam sayı }

Sonlu ve Sonsuz Küme

Eleman sayısı bir doğal sayı ile ifade edilebilen kümelere sonlu küme, edilemeyen kümelere sonsuz küme denir.

ÖRNEK: Aşağıdaki kümelerden hangilerinin sonlu hangilerinin sonsuz küme olduğunu belirleyelim.

► A = { a, b, c, ç } → A kümesi sonlu kümedir.

► B = { x | 12 < x , x bir tam sayı } → B kümesi sonsuz kümedir.

► C = { x | 1 < x < 33 , x bir doğal sayı } → C kümesi sonlu kümedir.

► D = { x | 1 < x < 33 , x bir rasyonel sayı } → D kümesi sonsuz kümedir.

ALT KÜME

A kümesinin her elemanı aynı zamanda B kümesinin de elemanı ise A kümesi B kümesinin alt kümesidir ve A \(\subset\) B ya da A \(\subseteq\) B ile gösterilir. Bu durumda B kümesi A kümesini kapsar. Bu ifade ise B \(\supset\) A ya da B \(\supseteq\) A ile gösterilir.

ÖRNEK: A = { 1, 2, 3 } ve B = { 0, 1, 2, 3, 4, 5 } kümelerini Venn şemasıyla gösterelim.

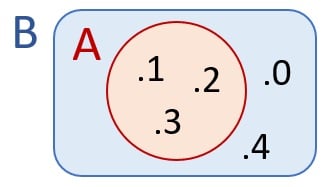
Venn şemasında da görüldüğü gibi A kümesinin her bir elamanı B kümesinin içinde yer almaktadır. Bu durum “A kümesi B kümesinin alt kümesidir (A \(\subset\) B) ” veya “B kümesi A kümesini kapsar, (B \(\supset\) A) ” şeklinde ifade edilir.

A kümesinin B kümesinden farklı en az bir tane elemanı varsa A kümesi B kümesinin alt kümesi değildir ve A \(\not\subset\) B ile gösterilir.

ÖRNEK: K = { a, b, c, ç } ve L = { a, d, e, f, c } kümeleri birbirinin alt kümesi değildir. K \(\not\subset\) L ve aynı zamanda L \(\not\subset\) K olur.

Alt Kümenin Özellikleri

► Boş küme her kümenin alt kümesidir. \(\varnothing \subset\) A

► Her küme evrensel kümenin alt kümesidir. A \(\subset\) E

► Her küme kendisinin alt kümesidir. A \(\subset\) A

► A, B ve C kümeleri için A \(\subset\) B ve B \(\subset\) C ise A \(\subset\) C’dir.

Alt Küme Sayısı

Eleman sayısı n olan bir kümenin alt küme sayısı 2ⁿ dir.

ÖRNEK: A = { 1, 2, 3 } kümesinin tüm alt kümelerini yazalım ve alt küme sayısını bulalım.

0 elemanlı alt kümeleri 1 tanedir. → { }

1 elemanlı alt kümeleri 3 tanedir. → {1} , {2} ve {3}

2 elemanlı alt kümeleri 3 tanedir. → {1,2} , {1,3} ve {2,3}

3 elemanlı alt kümeleri 1 tanedir. → {1,2,3}

A kümesinin toplam 8 alt kümesi vardır. Bu sayı kısaca 2³ = 8 şeklinde bulunabilir.

Öz Alt Küme Sayısı

Bir kümenin kendisi hariç alt kümelerine öz alt kümeleri denir. n elemanlı bir kümenin öz alt küme sayısı 2ⁿ − 1

ÖRNEK: A = { 1, 2, 3, 4, 5, 6 } kümesinin öz alt küme sayısı 2⁶ − 1 = 63 şeklinde bulunur.

EŞİT KÜME

Elemanları aynı olan kümelere eşit küme denir. A ve B kümelerinin eşitliği A = B ile gösterilir.

ÖRNEK: K = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 0 } ve L = { x | x , bir rakam } kümeleri eşit kümelerdir ve bu durum K = L şeklinde gösterilir.

NOT: Eşit olmayan A ve B kümeleri A \(\neq\) B şeklinde gösterilir.

ÖNCEKİ KONU	SONRAKİ KONU
Tanım, Aksiyom, Teorem ve İspat Kavramları	Kümelerde İşlemler