Rasyonel Sayılarla Çarpma İşlemi

BU KONUDA ÖĞRENECEKLERİMİZ:
√ Rasyonel Sayılarla Çarpma İşlemi
√ Çarpma İşleminin Özellikleri
√ Çarpma İşleminin Etkisiz Elemanı
√ Çarpma İşleminin Yutan Elemanı
√ Çarpma İşlemine Göre Ters Eleman
√ 0, 1 ve −1’in Etkisi

RASYONEL SAYILARDA ÇARPMA İŞLEMİ

Rasyonel sayılarda çarpma işlemi yaparken tam sayılarda çarpmada öğrendiklerimizi ve kesirlerde çarpmada öğrendiklerimizi kullanacağız. Kesirlerde öğrendiğimizin üzerine negatif sayılarla işlem yapmayı da öğreneceğiz.

Rasyonel sayılarda çarpma işlemi şunlara dikkat edilir:
∇ Çarpılan sayılarda tam sayılı kesir varsa bileşik kesre çevrilir.
∇ Çarpılan sayılarda tam sayı varsa paydasına 1 yazılır.
∇ Varsa sadeleştirme yapılır. Sadeleştirme yaparken çarpılan sayılarda paydaki herhangi bir sayı ile paydadaki herhangi bir sayı sadeleştirilebilir.
İşlem yapılırken:
∇ Çarpanlardaki paylar çarpılıp sonucun payına, paydalar çarpılıp sonucun paydasına yazılır.

ÖRNEK: \(\frac54\cdot\frac{-3}2\) işleminin sonucunu bulalım.

\(\frac54\cdot\frac{-3}2=\frac{5.(-3)}{4.2}=\frac{-15}8\) bulunur.

ÖRNEK: \(-2\frac13\cdot\frac{-2}7\) işleminin sonucunu bulalım.

Önce tam sayılı kesri bileşik kesre çeviriyoruz, sonra çarpma işlemini yapıyoruz.

\(-2\frac13\cdot\frac{-2}7=-\frac73\cdot\frac{-2}7=\frac{-14}{21}=\frac23\) olarak bulunur.

Ondalık gösterimi verilen sayıları rasyonel olarak yazdıktan sonra çarpma işlemi yapabiliriz.

ÖRNEK: \(-2.3,2\) işleminin sonucunu bulalım.

\(-2.3,2=\frac{-2}1\cdot\frac{32}{10}=\frac{-64}{10}=-\frac{32}5\) olur.

RASYONEL SAYILARDA ÇARPMA İŞLEMİNDE MODELLEME

Modelleme yapılırken çarpılan iki kesirden biri yatay biri dikey olarak ayrı ayrı modellenir ve üst üste konulur. İki renge de boyanmış küçük dikdörtgenlerin sayısının bütün dikdörtgenlere oranı da cevap olur.

ÖRNEK: \(\frac34\cdot\frac23=\frac6{12}\) işlemini modelleyelim.

Bir dikdörtgeni 4 satıra böler 3 tanesini boyarız, aynı boyutta başka bir dikdörtgeni 3 sütuna böler 2 tanesini boyarız.

Bu iki dikdörtgeni üst üste koyduğumuzda her iki renge boyanmış dikdörtgen sayısı pay, toplam dikdörtgen sayısı payda olur.

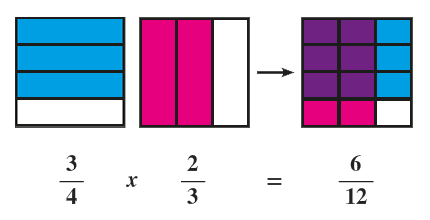
RASYONEL SAYILARDA ÇARPMA İŞLEMİNİN ÖZELLİKLERİ

DEĞİŞME ÖZELLİĞİ

Çarpılan sayıların yeri değişse de işlemin sonucu değişmediği için rasyonel sayılarda çarpma işleminin değişme özelliği vardır.

ÖRNEK: Değişme özelliğini şu şekilde gösterebiliriz

► \(\frac{-1}4\cdot\frac{-7}4=\frac{-7}4\cdot\frac{-1}4\)

BİRLEŞME ÖZELLİĞİ

İkiden fazla sayı çarpılırken parantez koyup önce iki tanesini çarpıp sonuçla diğerini çarpmak sonucu değiştirmez. Buna birleşme özelliği denir.

ÖRNEK: Birleşme özelliğini şu şekilde gösterebilir

► \(\left(\frac17\cdot\frac27\right)\cdot\frac{-5}7=\frac17\cdot\left(\frac27\cdot\frac{-5}7\right)\)

► \(\left(\frac2{49}\right)\cdot\frac{-5}7=\frac17\cdot\left(\frac{-10}{49}\right)\)
► \(\frac{-10}{343}=\frac{-10}{343}\)

DAĞILMA ÖZELLİĞİ

Çarpma işlemini toplama ve çıkarma işlemi üzerine dağıtabiliriz.

Aşağıdaki örnekte çarpmanın toplama üzerine dağılma özelliğini göstereceksiniz. Aynı şekilde aradaki işlem çıkarma olursa çarpmayı çıkrama üzerine dağıtırız.

► \(\frac1{22}\cdot\left(\frac{44}5+\frac{66}{10}\right)\)

► \(\left(\frac1{22}\cdot\frac{44}5\right)+\left(\frac1{22}\cdot\frac{66}{10}\right)\)

► \(\left(\frac1{22}\cdot\frac{\displaystyle22}5\right)+\left(\frac1{22}\cdot\frac{\displaystyle66}{10}\right)\)

► \(\frac25+\frac3{10}=\frac4{10}+\frac3{10}=\frac7{10}\)

ÇARPMA İŞLEMİNDE 1’İN ETKİSİ (ETKİSİZ ELEMAN)

Bir sayıyı 1 ile çarparsak sonuç sayının kendisi olur. Bu yüzden “1” çarpma işleminin etkisiz elemanıdır.

ÖRNEK: Etkisiz elemanı şu şekilde gösterebiliriz

► \(-\frac9{16}\cdot1=-\frac9{16}\)

ÇARPMA İŞLEMİNDE 0’IN ETKİSİ (YUTAN ELEMAN)

Bir sayıyı sıfır ile çarparsak sonuç “0” olur. Bu yüzden “0” çarpma işleminin yutan elemanıdır.

ÖRNEK: Yutan elemanı şu şekilde gösterebiliriz

► \(-\frac37\cdot0=0\)

ÇARPMA İŞLEMİNDE −1’İN ETKİSİ

Bir sayıyı −1 ile çarparsak sonuç o sayının toplama işlemine göre tersi olur.

ÖRNEK: Çarpma işleminde −1’in etkisini şu şekilde gösterebiliriz

► \(-\frac23\cdot\left(-1\right)=\frac23\)

ÇARPMA İŞLEMİNDE TERS ELEMAN

Çarpımları 1 olan iki rasyonel sayı çarpma işlemine göre birbirinin tersidir. Bir sayının çarpma işlemine göre tersini bulmak için pay ve paydasının yeri değiştirilir.

ÖRNEK: Bir sayının çarpma işlemine göre tersini şu şekilde gösterebiliriz

► \(-\frac56\) sayısının çarpma işlemine göre tersi \(-\frac65\) ‘tir.

Tam sayılı kesirlerin çarpma işlemine göre tersi bulunurken önce bileşik kesre çevrilir.

ÖRNEK: \(2\frac13\) ‘ün çarpma işlemine göre tersi \(\frac37\)‘dir.

Tam sayıların çarpma işlemine göre tersi bulunurken paydasına 1 yazılarak ters çevrilir.

\(-7\) ‘nin çarpma işlemine göre tersi \(-\frac17\) ‘dir.

√ Rasyonel sayılarla çarpma ve bölme işlemlerini yapar.

ÖNCEKİ KONU	SONRAKİ KONU
Rasyonel Sayılarla Toplama ve Çıkarma	Rasyonel Sayılarla Bölme